Question

bridge is in the shape of a semi – ellipse. It is 400 metres long and has a maximum height of 10 metres at the middle point. The height of the bridge at a point at a distance of 80 metres from one end is:
(a) 4 metres
(b) 2 metres
(c) 8 metres
(d) $\sqrt{91}\text{ metres}$

Answer 1

Hint: We are going to use the equation of an ellipse i.e. $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{b}=1$ where “a” and “b” are the length of semi major and semi minor axis respectively. In the given problem, the semi major axis is half of 400 m and the semi minor axis is given as 10 m. Now, substitute the values of “a” and “b” in the equation of an ellipse. Now, to find the height of the bridge which is at 80 m from one end so the distance from the centre of half of the ellipse is the subtraction of 80 from 200 then we get the value of “x” in the equation of the ellipse. Substituting this value of x in the ellipse will give us the value of y. Hence, this value of “y” is the height of the bridge at a point at a distance of 80 metres from one end.

Complete step-by-step answer:
We have given a bridge in the form of a semi – ellipse which is 400 m long and the maximum height at the middle point is 10 m. In the below diagram, we have shown a semi ellipse with semi minor axis as “a” and semi major axis as “b”.

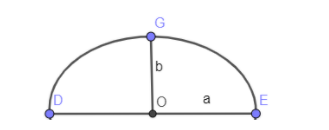
In the above diagram, $\text{OE}=a$ and $\text{OG}=b$. From the information given in the question the length of the major axis is given as 400 m so the semi major axis is the half of 400 m which is 200 m. The maximum height of the bridge at mid point which is the point O in the above diagram is the length of minor axis which is 10 m.
We know that the equation of an ellipse is equal to:
$\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$…………. Eq. (1)
In the above formula, “a” represents semi major axis and “b” represents semi minor axis. In the above, we have shown the value of “a” is 200 m and the value of “b” is 10 m. Substituting these values of “a” and “b” in the above equation we get,
$\dfrac{{{x}^{2}}}{{{\left( 200 \right)}^{2}}}+\dfrac{{{y}^{2}}}{{{\left( 10 \right)}^{2}}}=1$………. Eq. (2)
We are asked to find the height of the bridge at the distance of 80 m from one end. In the above formula of the equation of an ellipse, x and y are the distance from the point O shown in the above figure.
In the below diagram, we have shown DF as 80 m and the height of the bridge at point F is HF.

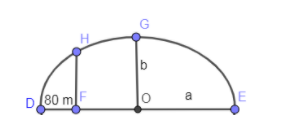
In the above diagram, $\text{OD}=200m$ so $FO=200-80=120m$. Substitute the value of FO in place of x in the eq. (2) we get,
$\begin{align}
  & \dfrac{{{\left( 120 \right)}^{2}}}{{{\left( 200 \right)}^{2}}}+\dfrac{{{y}^{2}}}{{{\left( 10 \right)}^{2}}}=1 \\
 & \Rightarrow \dfrac{14400}{40000}+\dfrac{{{y}^{2}}}{{{\left( 10 \right)}^{2}}}=1 \\
 & \Rightarrow \dfrac{144}{400}+\dfrac{{{y}^{2}}}{{{\left( 10 \right)}^{2}}}=1 \\
 & \Rightarrow \dfrac{36}{100}+\dfrac{{{y}^{2}}}{100}=1 \\
\end{align}$
Subtracting $\dfrac{36}{100}$ on both the sides we get,
$\dfrac{{{y}^{2}}}{100}=1-\dfrac{36}{100}$
$\begin{align}
  & \dfrac{{{y}^{2}}}{100}=\dfrac{64}{100} \\
 & \Rightarrow {{y}^{2}}=64 \\
\end{align}$
Taking square root on both the sides we get,
$y=8$
From the above equation, the value of HF is equal to 8 m.
Hence, the correct option is (c).

Note: There is an interesting point to be noted in the above problem is that while taking the square root of the following equation in the above problem we take only the positive solution.
$\begin{align}
  & {{y}^{2}}=64 \\
 & \Rightarrow y=8 \\
\end{align}$
The reason for taking the positive solution is because the bridge is swinging in the sky so the height of the bridge must be positive so we have rejected the negative solution of y.