Question

Calculate the angular and linear speed of the 2nd hand of the clock of length \[7cm\] .

Answer 1

Hint:
We all know the clock has 3 hands. The hour hand, the minute hand and the second hand. The minute hand is the 2nd hand which takes 1 hour to complete its one circle of rotation. Similarly the hour hand and second hand take 12 hours and 1 minute to complete one rotation.

Complete step by step answer:
We know that in circular motion, angular speed or velocity is a completely different physical quantity than angular speed.
Let’s look at the following diagram.

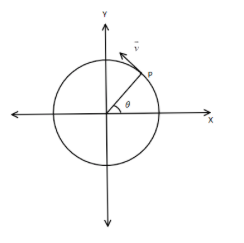
A particle in motion P, has an angular displacement of $\theta $ for a time period of complete rotation $t$ .
Angular velocity is defined as rate of change of angular positions $\theta $ , that is $\omega = \dfrac{{d\theta }}{{dt}}$
Where $d\theta $ and $dt$ are the changes in angular displacement and time respectively.
The unit of angular velocity is $rad{s^{ - 1}}$
The linear velocity of the particle P is displacement per unit time or $v = \dfrac{{ds}}{{dt}}$
Where $ds$ is the change in position/displacement of the particle.
Linear velocity is related to angular velocity by the following equation,
$v = r\omega $ , where $r$ is the radius of the circular trajectory the particle exhibits.
As the second hand of the clock, that is, the minute hand takes 1 hour to complete a full rotation ( a full rotation means angular displacement of $2\pi rad$ .
Thus the angular velocity will be, $\omega = \dfrac{{2\pi }}{{3600}}$
Because 1 hour converted to seconds is $3600s$
$ \Rightarrow \omega = 5.48 \times {10^{ - 3}}rad.{s^{ - 1}}$
Now, the linear velocity of the 2^nd hand of the clock will be,
$v = r\omega $
Given that the length of the 2^nd hand is $7cm$ or $0.07m$. Substituting the values of $\omega $ and $r$ we get,
$v = 0.07 \times 5.48 \times {10^{ - 3}}$
$ \Rightarrow v = 3.8 \times {10^{ - 4}}m{s^{ - 1}}$
This is the value of linear velocity of the tip of the 2^nd hand of the clock.

Note: Make sure you are doing calculations in the same system of units. While converting use power of 10 values for easier calculations. We can similarly calculate the angular and linear velocities of 1^st and 3^rd hands of a clock such that their time period for a complete rotation around the clock is 12 hours and 1 minute respectively.