Question

Calculate the area of quadrilateral ABCD in which AB= 32cm, AD = 24cm, $\angle A$=${90^ \circ }$and BC = CD = 52cm.
A) $1344\,c{m^2}$
B) $1433\,c{m^2}$
C) $1300\,c{m^2}$
D) $1540\,c{m^2}$

Answer 1

Hint: Now there is no set formula for finding the area of quadrilateral in geometry. So, we will draw the quadrilateral as a combination of triangles and find the areas of those triangles to get the area of the quadrilateral.

Complete step by step answer:

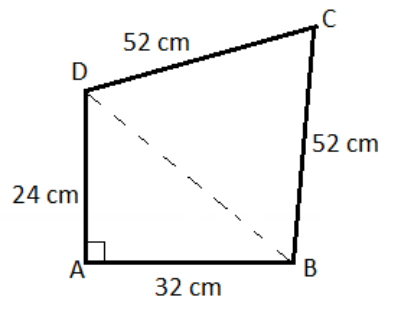
Now, from the diagram clearly we can say that the quadrilateral ABCD is a combination of two triangles $\Delta ADB$ and $\Delta DBC$, out of which $\Delta ADB$ is a right angled triangle right angled at A according to the question.
Then, we can say from the diagram that-
Area of quadrilateral ABCD = Area of $\Delta ADB$+Area of$\Delta DBC$
Now, since $\Delta ADB$ is a right angled triangle,
So Area of Right Angled triangle is given as = $\dfrac{1}{2} \times base \times height$
In $\Delta ADB$, base = AB = 32cm, while the height is AD = 24cm.
So, substituting these values we will get
Area of Right Angled triangle $\Delta ADB$=
$
  \dfrac{1}{2} \times base \times height \\
   = \dfrac{1}{2} \times 32 \times 24 \\
   = 16 \times 24 \\
   = 384\,c{m^2} \\
$
Next we need to find the Area of $\Delta DBC$.
Now, $\Delta DBC$ is not a right angled triangle but an isosceles triangle with two equal sides CD = BC = 52cm.
So to find the area of $\Delta DBC$ we will first need to find the length of BD, so that we can find the area of $\Delta DBC$ using Heron’s Formula.
Now to find BD, we will apply Pythagoras theorem in $\Delta ADB$.
Now, Pythagoras theorem says that:
${\left( {hypotenuse} \right)^2} = {\left( {base} \right)^2} + {\left( {perpendicular} \right)^2}$
So, substituting base AB= 32cm and perpendicular AD= 24cm we will get the hypotenuse BD as:
$
  B{D^2} = A{B^2} + A{D^2} \\
   = {\left( {32} \right)^2} + {\left( {24} \right)^2} \\
   = 1024 + 576 \\
   = 1600cm \\
$
Then,
$
  B{D^2} = 1600cm \\
   \Rightarrow BD = \pm 40cm \\
$
Since, measurement can never be negative, so BD comes out to be 40cm.
Now in $\Delta DBC$, we have CD=BC=52cm and BD = 40cm,
So according to Heron’s Formula
The semi-perimeter $s = \dfrac{{a + b + c}}{2}$ where a,b and c are the three respective sides of a triangle.
So for $\Delta DBC$,
$
  s = \dfrac{{52 + 52 + 40}}{2} \\
   = \dfrac{{144}}{2} \\
   = 72cm \\
$
Now Heron’s formula for area of a triangle is given as:
$\sqrt {s(s - a)(s - b)(s - c)} $
Now, substituting the value of ‘s’ we have just now calculated in the previous step and the values of all the three sides of the triangle we will get the
Area of $\Delta DBC$= $\sqrt {s(s - a)(s - b)(s - c)} $
$
   = \sqrt {72(72 - 52)(72 - 52)(72 - 40)} \\
   = \sqrt {72 \times 20 \times 20 \times 32} \\
   = \sqrt {8 \times 9 \times 20 \times 20 \times 8 \times 4} \\
   = 8 \times 3 \times 20 \times 2 \\
   = 960\,c{m^2} \\
$
So, now adding the areas of both the triangles, $\Delta ADB$ and $\Delta DBC$, we will get the area of quadrilateral ABCD.
Hence, Area of quadrilateral ABCD = Area of $\Delta ADB$+Area of $\Delta DBC$
$
   = 960\,c{m^2} + 384\,c{m^2} \\
   = 1344\,c{m^2} \\
$
Therefore, the correct answer is Option A.

Note: The formula for finding areas of different triangles is different. We use Heron’s formula to find the areas of triangles,in which none of the sides are equal. Now the perimeter of a triangle is the sum of all three sides, while semi-perimeter is the half of this perimeter, denoted by: $s = \dfrac{{a + b + c}}{2}$ where a,b and c are the three respective sides of the triangle.
The usual formula used for calculating the area of the triangle is $\dfrac{1}{2} \times base \times height$ . The Heron’s formula for a triangle is given as: $\sqrt {s(s - a)(s - b)(s - c)} $.