Question

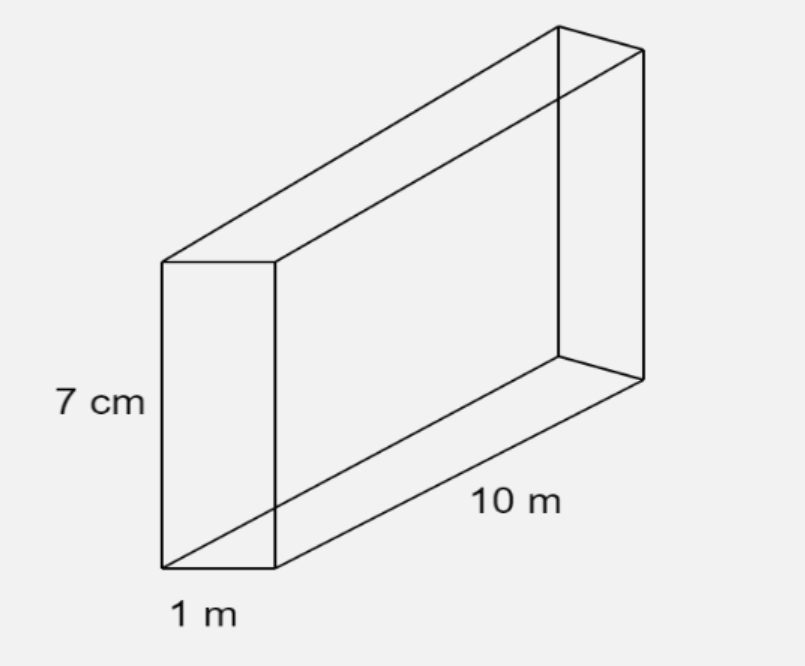
Calculate the total surface area of the cuboid shown in the below figure.

Answer 1

Hint: We know that the cuboid is made up of \[6\] rectangles. So, the total surface area of a cuboid is equal to the area of all \[6\] rectangles. Also, we can see that the dimensions are in different units. So we will convert all the dimensions into \[cm\]. Then we will put the values of length, breadth and height into the formula for calculating the total surface area.

Formula used:
Total surface area of a cuboid \[ = 2\left( {lb + bh + hl} \right)\]
\[l = {\text{ length}}\]
\[b = {\text{ breadth}}\]
\[h = {\text{height}}\]

Complete step by step answer:
Given

\[l = 10{\text{ m}}\]
\[b = 1{\text{ m}}\]
\[h = 7{\text{ cm}}\]
We can see that length and breadth are given in meters and height is given in centimetres. So, we will convert the length and breadth into centimetres. So,
\[l = 10{\text{ m}}\]
\[ \Rightarrow l = 1000{\text{ cm}}\]
\[b = 1{\text{ m}}\]
\[ \Rightarrow b = 100{\text{ cm}}\]
Now since all the dimensions are in the same unit, we will put these values into the formula for calculating the total surface area of the cuboid.
Total surface area of cuboid \[ = 2\left( {lb + bh + hl} \right)\]
Putting the values of length, breadth and height. We get,
Total surface area of cuboid \[ = 2\left\{ {\left( {1000{\text{ cm }} \times 100{\text{ cm}}} \right) + \left( {100{\text{ cm }} \times 7{\text{ cm}}} \right) + \left( {7{\text{ cm }} \times 1000{\text{ cm}}} \right)} \right\}\]
\[ = 2\left[ {100000 + 700 + 7000} \right]{\text{ c}}{{\text{m}}^2}\]
\[ = 2\left( {107,700} \right){\text{ c}}{{\text{m}}^2}\]
\[ = 215,400{\text{ c}}{{\text{m}}^2}\]
Therefore, the total surface area of the cuboid is \[215,400{\text{ c}}{{\text{m}}^2}\].

Note:
One mistake that most of the students commit in these types of questions is that they do not see whether the given dimensions are in the same units or not. Before putting the dimensions into the formula, we need to convert all of them into the same units. Another point to note is that we can also solve the given question by changing all the dimensions into meters. Also, it is important that we put the unit of area in the final answer.