Question

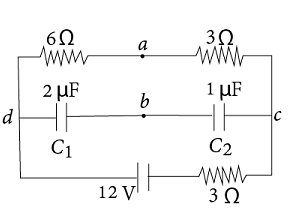
What is the charge stored on each capacitor \[C_1\] and \[C_2\]​ in the circuit shown in figure?

(a). $6\mu C,6\mu C$
(b). $6\mu C,3\mu C$
(c). $3\mu C,6\mu C$
(d). $3\mu C,3\mu C$

Answer 1

- Hint: Though we know that the charge on the capacitor varies with the time but here we see in the options; the charges are discrete and fixed so after coming to this discussion we can say that this situation given in the question is the case of the steady state. In such situations we always assume the steady state.

Complete step-by-step solution -
Now we have to find that in the steady state what are the charges stored in both the capacitors in the circuit.
Steady state means the capacitors are fully charged, and when the capacitors are fully charged then the current will not flow through the capacitor. So, the current through the branch $dc$ is zero.
We have to find the potential difference between the points $d$ and $c$.
Let the current flowing in the circuit $ = i$
Now applying the Kirchhoff’s law for the larger loop,
$ + 12 - 6i - 3i - 3i = 0$
$ \Rightarrow - 12i = - 12$
$ \Rightarrow i = 1A$
So, like this we have got the current flowing in the circuit, that is $i = 1A$.
So $1A$ current is flowing in the steady state.
Now for getting the potential difference across the branch $dc$ we will follow the procedure as following
We see that both the capacitors are connected to each other in series, so the same charges will appear on both the capacitors.
So, let the acquired charges on the capacitors $ = q$
Now applying the Kirchhoff’s law for the lower loop,
$ + 12 - \dfrac{q}{{{C_1}}} - \dfrac{q}{{{C_2}}} - 3i = 0$
$ \Rightarrow + 12 - \dfrac{q}{{{C_1}}} - \dfrac{q}{{{C_2}}} - 3 \times 1 = 0$
$ \Rightarrow - q(\dfrac{1}{{{C_1}}} + \dfrac{1}{{{C_2}}}) = - 9$
It is given ${C_1} = 2\mu F$and ${C_2} = 1\mu F$
So, putting these values,
$ \Rightarrow q(\dfrac{1}{2} + \dfrac{1}{1}) = 9$
$ \Rightarrow q = \dfrac{{9 \times 2}}{3}$
$ \Rightarrow q = 6\mu C$
Hence the charges that will appear on both the capacitors will be $6\mu C$.
So, option (a) is the correct answer.

Note-Kirchhoff’s circuit law is described by the German physicist Gustavo Kirchhoff in $1845$. Kirchhoff circuit law is actually two laws, Kirchhoff’s current law and Kirchhoff’s voltage law. Kirchhoff current law says that the sum of the current entering and leaving through a node is zero and Kirchhoff voltage law says that the sum of the voltage across any loop of the circuit is zero.