
Complete the following statement : The smallest 7 digit number is_____
a). 1000000
b).
c). Both A and B
d). 999999
Answer
522k+ views
Hint: We will find the smallest 7 digit number using natural numbers and the number line. The numbers which are in the left side of the number line are smaller and the numbers which are in the right side of the number line are greater numbers. For example in case of numbers
Complete step-by-step solution -
It is given in the question that we have to find the smallest 7-digit number. We will take help from the number line to find the smallest 7-digit natural numbers. We know that on the number line the number which is on the left side is a smaller number than the number which is on the right side. For example, we are taking three numbers 6,7 and 8 and when we represent them on a number line, we see that 6 is in the most left side among three numbers thus 6 is the smallest number in these three numbers. 8 is on the most right side among these three numbers thus, 8 is the largest number among these three numbers. Or we can say that according to the representation of numbers on the number line, we get
Now we will try to find out the smallest 7 digit number using the number line. Before finding the smallest 7-digit number we will find the length 6-digit number. So, the largest 6-digit number is 999999. Now, we will try to find out the next number on the right side of 999999.
So, the number which is next to the number 999999 is 1000000 which is a 7-digit number. When we represent these three numbers on the number line, we get –
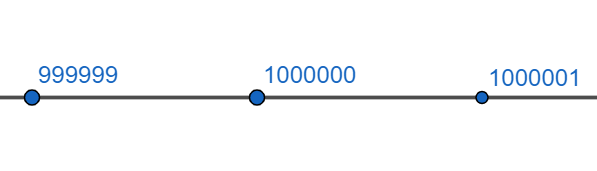
Also, with the help of the number line, we can say that
Note: The smallest natural number is 1 and the largest 1 digit natural number is 9. Similarly we have the smallest 2 digit number as 10 and the largest 2 digit number as 99, and so on. So, the conclusion is that the number starting with 1 and ending with recurring 0 are the smallest number of the group of the same digits like 1 in 1 digit and 10 in 2 digit and 100 in 3 digit and so on. Similarly the numbers starting with 9 and ending with recurring 9 are the largest number of their group of the same digit, like 9 in 1 digit, 99 in 2 digit, 999 in 3 digit, and so on.
Complete step-by-step solution -
It is given in the question that we have to find the smallest 7-digit number. We will take help from the number line to find the smallest 7-digit natural numbers. We know that on the number line the number which is on the left side is a smaller number than the number which is on the right side. For example, we are taking three numbers 6,7 and 8 and when we represent them on a number line, we see that 6 is in the most left side among three numbers thus 6 is the smallest number in these three numbers. 8 is on the most right side among these three numbers thus, 8 is the largest number among these three numbers. Or we can say that according to the representation of numbers on the number line, we get
Now we will try to find out the smallest 7 digit number using the number line. Before finding the smallest 7-digit number we will find the length 6-digit number. So, the largest 6-digit number is 999999. Now, we will try to find out the next number on the right side of 999999.
So, the number which is next to the number 999999 is 1000000 which is a 7-digit number. When we represent these three numbers on the number line, we get –

Also, with the help of the number line, we can say that
Note: The smallest natural number is 1 and the largest 1 digit natural number is 9. Similarly we have the smallest 2 digit number as 10 and the largest 2 digit number as 99, and so on. So, the conclusion is that the number starting with 1 and ending with recurring 0 are the smallest number of the group of the same digits like 1 in 1 digit and 10 in 2 digit and 100 in 3 digit and so on. Similarly the numbers starting with 9 and ending with recurring 9 are the largest number of their group of the same digit, like 9 in 1 digit, 99 in 2 digit, 999 in 3 digit, and so on.
Latest Vedantu courses for you
Grade 10 | CBSE | SCHOOL | English
Vedantu 10 CBSE Pro Course - (2025-26)
School Full course for CBSE students
₹37,300 per year
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Difference Between Plant Cell and Animal Cell

Given that HCF 306 657 9 find the LCM 306 657 class 9 maths CBSE

The highest mountain peak in India is A Kanchenjunga class 9 social science CBSE

What is the difference between Atleast and Atmost in class 9 maths CBSE

What is pollution? How many types of pollution? Define it




