Question

Complete the hierarchy using the categories below. Write a category in each box to complete the tree diagram

Answer 1

Hint: This question will be solved by the knowledge of sides of shape of each given term. Recall the definitions of each of the figures given in the question and then check which figure can satisfy the conditions of other figures as well.

Complete step-by-step answer:
We have Rectangles, Squares, trapezoids, polygons, rhombuses, quadrilaterals and parallelograms.
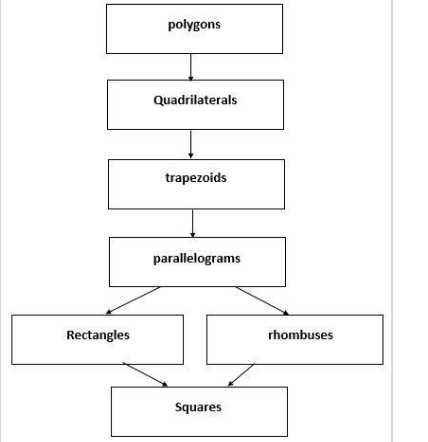
Polygon can be any closed figure joined by straight lines. So clearly, all the rest figures given in the question are polygons.
Therefore, the polygon will be set at the top of the hierarchy.
Then we have Rectangles, Squares, trapezoids, rhombuses, quadrilaterals and parallelograms.
All the figures have four sides. Any figure with four sides is called quadrilateral.
Therefore, quadrilateral will be the next in line.
Then we have Rectangles, Squares, trapezoids, rhombuses and parallelograms.
Trapezoids are figures with two sides parallel to each other. So every rectangle, square, rhombus and parallelogram is a trapezoid.
Therefore, trapezoid will be next in the line.
Now we have Rectangles, Squares, rhombuses and parallelograms.
In parallelogram, opposite sides are parallel and equal. So, every rectangle, square and rhombus is a parallelogram.
Therefore, parallelogram will be next in the line.
Then we have Rectangles, Squares and rhombuses.
Now, rectangle is a quadrilateral whose all angles are
Thus, a rhombus is not necessarily a rectangle, because in rhombus, opposite angles are equal but not necessarily equal to
Also, all the sides of a rhombus are equal but all the sides of a rectangle are not necessarily equal.
Therefore, a rhombus is not necessarily a rectangle.
Thus, rhombus and rectangle cannot be placed under each other.
Thus, they should be placed parallel to each other.
Since, all the angles of a square are equal to and all the sides of a square are equal and parallel to opposite sides, a square is a rectangle as well as a rhombus.
Thus, from the above explanation, we can fill the given table of hierarchy as,

Note: To solve this question you must have the knowledge of the properties of all the given figures. Placing the rectangle and rhombus parallel could be tricky. You need to understand that rectangles and rhombus cannot be placed under each other. And you should also understand that rectangles and rhombus both include squares. Trapezoids and trapezium are the same thing. Do not get confused with it.