Question

Consider an electric field $\bar E = {E_0}\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x} $ where ${E_0}$ is a constant. The flux through the shaded area as shown in this field is

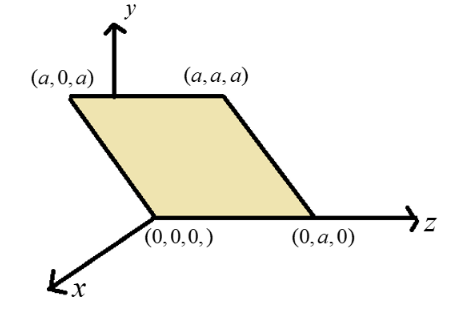
(A) $2{E_0}{a^2}$
(B) $\sqrt 2 {E_0}{a^2}$
(C) ${E_0}{a^2}$
(D) $\dfrac{{{E_0}{a^2}}}{{\sqrt 2 }}$

Answer 1

Hint: We can solve the given problem with the help of the magnitude of the electric field. The magnitude of the electric field can be determined by Coulomb's force.

Formula used: Electric flux through an area is, $\phi = \vec E.d\vec S = EdS\cos \theta $

Complete step-by-step answer:
Let us first write the information given in the question.
Electric field is applied along x-axis and it is a constant electric field,
$\vec E = {E_0}\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x} $

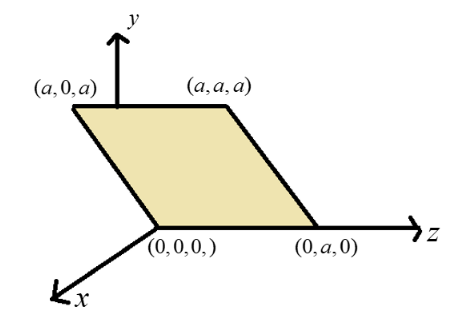
Let us make use of the diagram and find the angle between electric field and normal to the shaded surface. We can see that the shaded surface is tilted at 45o to x-axes. That means,
\[\;\theta = {45^o}\] (1)
Now let us calculate the surface area of the shaded region. The shaded region is a parallelogram of side a. The area of parallelogram is given below.
\[{\text{A = base x height}}\] (2)
Again, using the figure, base= $a$ and height= $\sqrt a $.
Now, let us substitute the values in (2) and we get the following.
\[A = a \times \surd 2a\]
 \[ \Rightarrow \surd 2{\text{ }}{a^2}\] (3)
Magnitude of the electric field is given below.
$\left| {\vec E} \right| = {E_0}$ (4)
Now, let calculate the flux through shaded region using the formula
 $\phi = \vec E.d\vec S$
$ \Rightarrow EdS\cos \theta $
Let us substitute the values from equation (1). (3) and (4).
$\phi = {E_0} \times \sqrt 2 {a^2}\cos 45$
Let us further simplify it.
$\phi = {E_0} \times \sqrt 2 {a^2} \times \dfrac{1}{{\sqrt 2 }}$
$ \Rightarrow \phi = {E_0}{a^2}$

Hence, option (C) “${E_0}{a^2}$” is correct option

Note: Electric field strength is measured in terms of electric field lines. So, electric flux is defined as the number of field lines passing through an area and this depends on the angle between electric field and normal to the surface.
Therefore, electric flux passing through a surface will be large, when normal to the surface and field lines are parallel to each other.
Another method is, resolve the area vector in its x and y component.
Then take its dot product with an electric field, only x component will remain.