Question

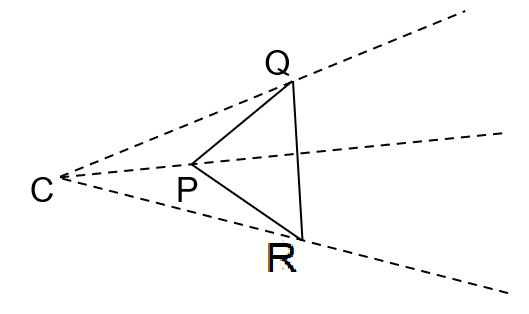
Construct a dilation, with scale factor 2, of a triangle using only a ruler and compasses.

Answer 1

Hint: We use the centre of dilatation to join the given triangle. Then we use two processes of reduction and enlargement to find the required triangles. The conditions to do the dilation is \[C{{P}^{''}}< CP,C{{Q}^{''}}< CQ,C{{R}^{''}}< CR\] and $C{{P}^{'}}=2CP, C{{Q}^{'}}=2CQ, C{{R}^{'}}=2CR$ respectively.

Complete step-by-step solution:
We follow some steps for the dilation process to dilate $\Delta PQR$ by a scale factor of 2 with a center of dilation at point C.
Step: 1
We connect the center of dilation C to each vertex and extend those lines.
Step: 2
Then we place the point of the compass on the center of dilation C and the pencil on vertex Q to measure the distance.
Step: 3
Now, without changing the size of the compass, we will move the point of the compass to vertex Q, and make a mark on the line of extended CQ.
Step: 4
We now repeat the process for each of the other vertices of the triangle. Let’s assume the new vertices are ${{P}^{'}},{{Q}^{'}},{{R}^{'}}$. So, $C{{P}^{'}}=2CP,C{{Q}^{'}}=2CQ,C{{R}^{'}}=2CR$.
Step: 5
We connect the points ${{P}^{'}},{{Q}^{'}},{{R}^{'}}$ to get the triangle.

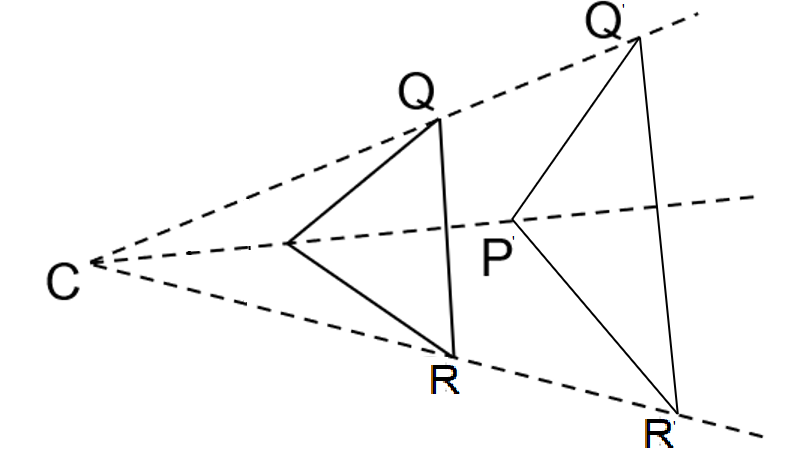
The above process was enlargement and now we do the reduction.
Step: 1 Now to get the triangle in between the point C and given $\Delta PQR$, we take our scale factor as less than 1 to reduce size.
Step: 2 We will set our compass to a distance that is more than halfway between vertex P and points C. Step: 3 Keeping the compass at that same distance, we draw a curve that intersects the line between P and C. We do the same thing for all other points. Let’s assume the new vertices are ${{P}^{''}},{{Q}^{''}},{{R}^{''}}$. So, \[C{{P}^{''}}< CP,C{{Q}^{''}}< CQ,C{{R}^{''}}< CR\].
Step: 4 We connect the points ${{P}^{''}},{{Q}^{''}},{{R}^{''}}$ to get the triangle.

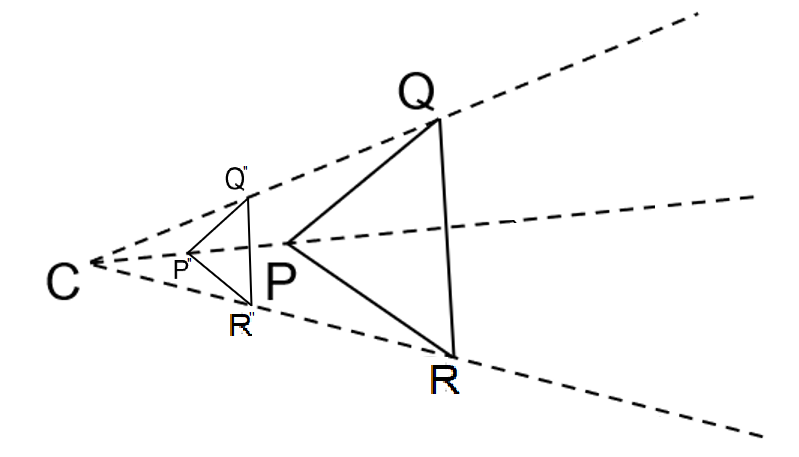
Note: We need to remember that one process is enough to show the dilation. This process is used to minimize and maximize the size of the triangle keeping all the respective side and angles ratios the same. These triangles are called similar triangles.