
Construct a trapezium KITE in which
Answer
453.6k+ views
Hint: Firstly, we have to draw the base KI of the trapezium of length
Complete step by step solution:
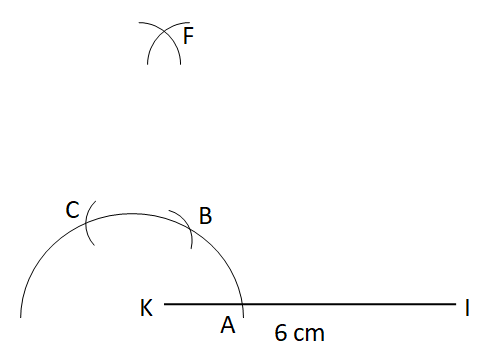
Step I: Draw the base KI of length
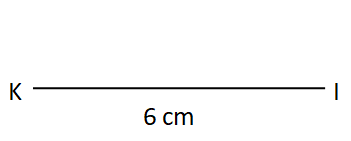
Step II: With K as centre a convenient radius, draw an arc.
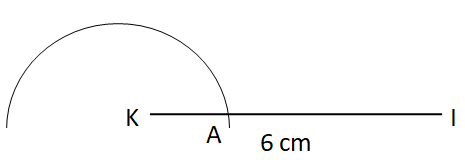
Step III: Now, with A as centre and the same radius, draw an arc cutting the original arc at B.
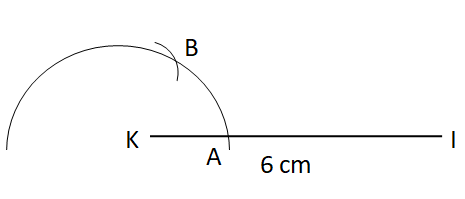
Step IV: With B as centre and the same radius, draw an arc cutting the original arc at C.
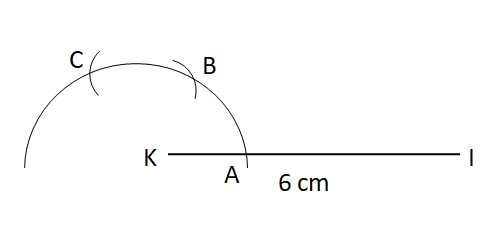
Step V: Now, with B and C as centers and the same radius, draw two arcs cutting each other at D.
Step VI: With B and F as centers and same radius, draw two arcs cutting at G to obtain the angle of
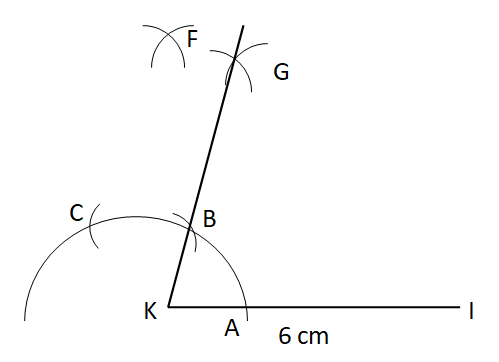
Step VII: Similarly, draw an angle of
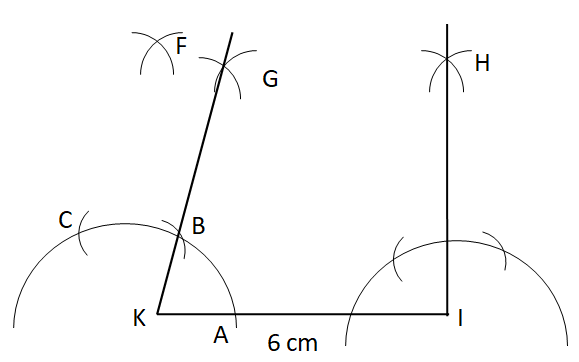
Step VIII: With the help of the ruler, mark the points E on KG at the distance of
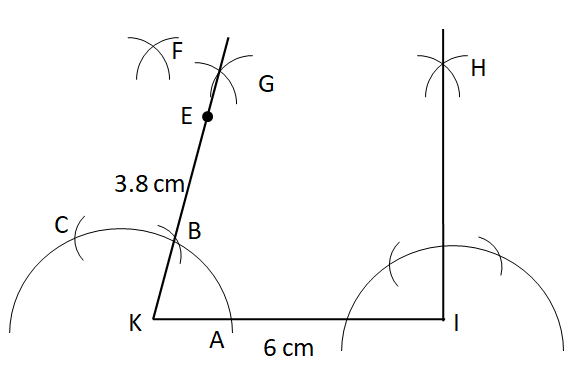
Step IX: With E as centre and radius
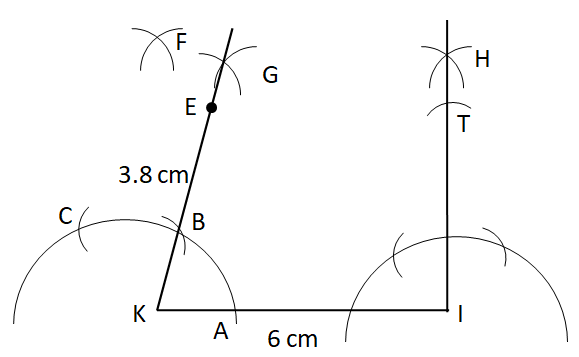
Step X: Finally, join E and T.
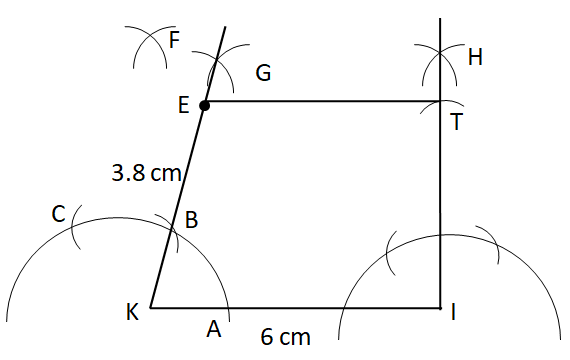
Hence, the trapezium KITE is constructed.
Note: In the given question, the angle T is given to be equal to
Complete step by step solution:
Step I: Draw the base KI of length

Step II: With K as centre a convenient radius, draw an arc.

Step III: Now, with A as centre and the same radius, draw an arc cutting the original arc at B.

Step IV: With B as centre and the same radius, draw an arc cutting the original arc at C.

Step V: Now, with B and C as centers and the same radius, draw two arcs cutting each other at D.

Step VI: With B and F as centers and same radius, draw two arcs cutting at G to obtain the angle of

Step VII: Similarly, draw an angle of

Step VIII: With the help of the ruler, mark the points E on KG at the distance of

Step IX: With E as centre and radius

Step X: Finally, join E and T.

Hence, the trapezium KITE is constructed.
Note: In the given question, the angle T is given to be equal to
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Difference Between Plant Cell and Animal Cell

Given that HCF 306 657 9 find the LCM 306 657 class 9 maths CBSE

The highest mountain peak in India is A Kanchenjunga class 9 social science CBSE

What is the difference between Atleast and Atmost in class 9 maths CBSE

What was the capital of the king Kharavela of Kalinga class 9 social science CBSE




