Question

How do we construct a triangle equal in area to a given triangle or quadrilateral?

Answer 1

Hint: In this problem, we have to construct a triangle equal in area to a given triangle or quadrilateral. We can construct a triangle equal in area to a given triangle by drawing a line parallel to the base of the triangle and joining the point of the base and the point on the parallel line to get triangles equal in area of the given triangle.

Complete step-by-step solution:
We have to construct a triangle equal in area to a given triangle or quadrilateral.
Let us assume that ABC is a given triangle.
We are to construct a triangle equal in area to this triangle in step by step.
Let us first draw a triangle ABC. Then we will get

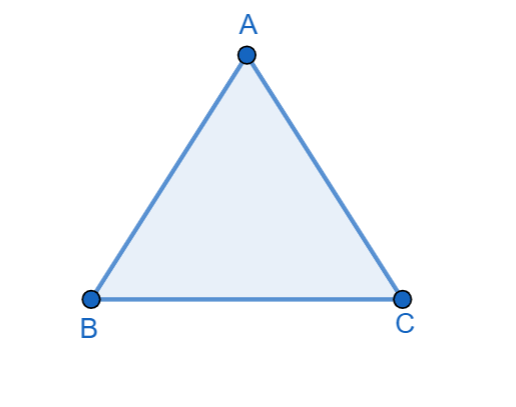
Now, let us draw a line parallel to the base of the triangle BC. For this first let us consider a point A above the base. Now, by taking a suitable radius we will draw an arc with center B which cuts the line segment AB at F and BC at G. Then we will get

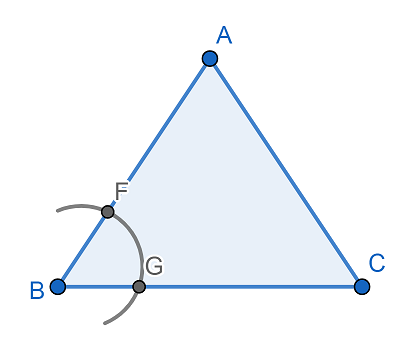
Now, taking the same radius with A as center we will cut the line segment AB at R. Then we will get

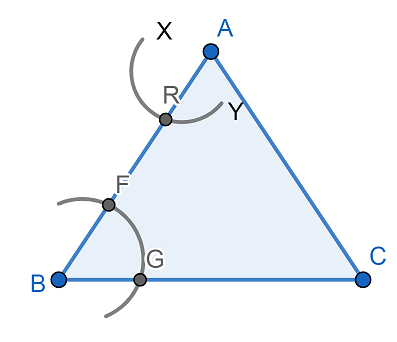
Now, again taking the same radius as previously used we will cut the arc XY at S from the center R. Then we will get

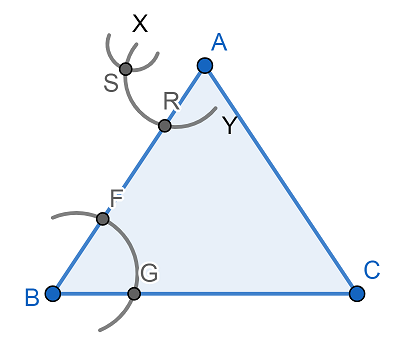
Now, joining the points A and S and drawing a line segment we will get

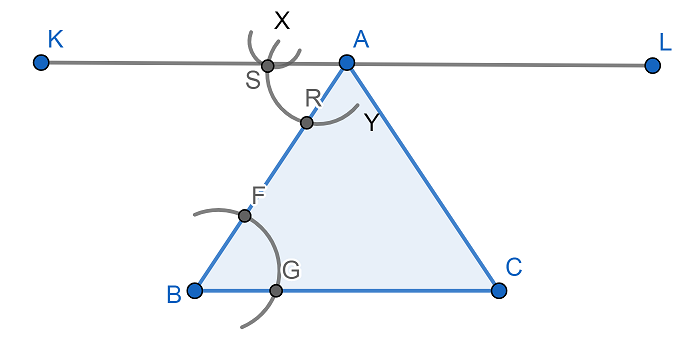
Now, KL is the required line segment parallel to line segment BC.
Now, we can draw points on the line segment KL and join the points with base BC to get the triangle equal in area to the triangle ABC. Then we will get

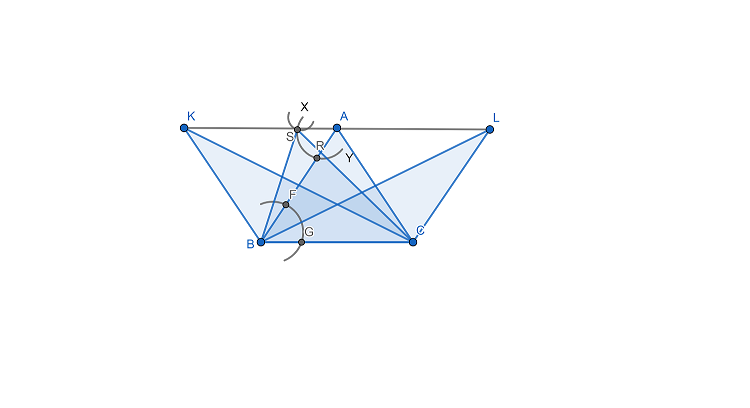
Therefore, we get three triangles $\Delta KBC,\Delta XBC,\Delta LBC$which are equal to the area of \[\Delta ABC\].

Note: The point to be remembered is that if we place triangles between two parallel straight lines then the area of all triangles with the same base will be equal. Students make mistakes while joining the two points in the base and the point on the parallel line, in which we should concentrate. We can also construct a quadrilateral from the triangle of the same area.