Question

Construct a triangle of sides 4 cm, 5cm, and 6cm and then a triangle similar to it whose sides are \[\dfrac{2}{3}\] of the corresponding sides of the first triangle.

Answer 1

Hint: Here first we will construct the triangle with sides 4 cm, 5cm, and 6cm and then we will use the given fraction of the side to construct a similar triangle.

Complete step by step answer:
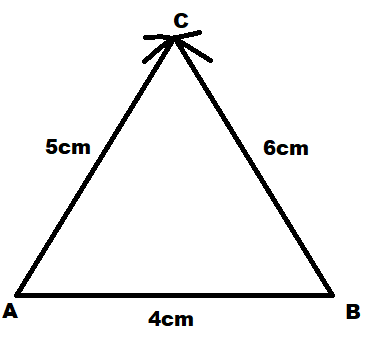
Let us first draw the triangle with sides 4 cm, 5cm and 6cm.
- First, we will draw the base AB of the triangle of length 4cm.
- Then A as the center we will mark an arc with the help of a compass at a distance of 5cm.
- Similarly, now with B as the center, we will mark an arc with the help of a compass at a distance of 6cm.
- Now finally we will mark the point so obtained as C and then join the points A and C and A and B.

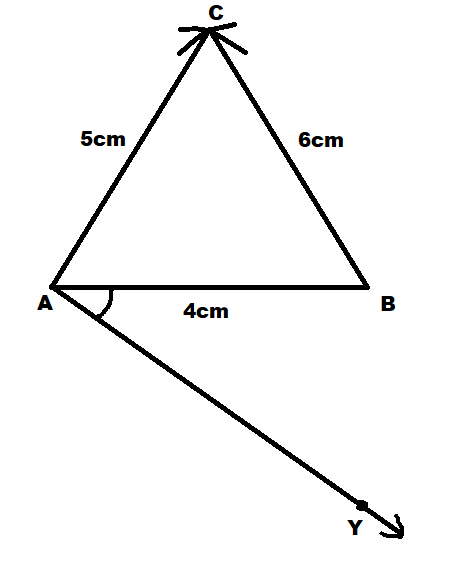
Now we will construct a similar triangle of ABC whose sides are \[\dfrac{2}{3}\] of the corresponding sides of \[\Delta ABC\].
We will first construct a ray AY such that it makes an acute angle with line AB on the opposite side of vertex C.

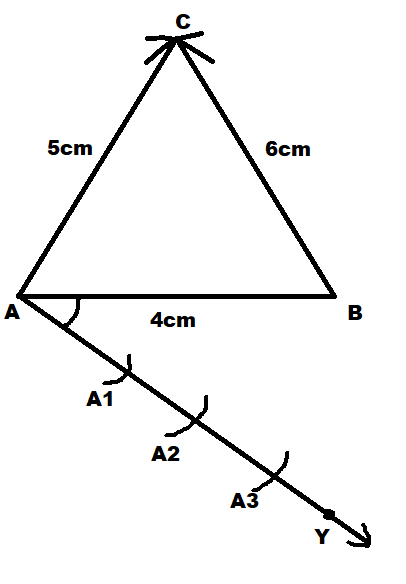
Now we will mark three points at equal distances from each other on the ray AY i.e. \[A{A_1} = {A_1}{A_2} = {A_2}{A_3}\]

Now we will join \[{A_3}\] to \[B\] and then we will draw a line \[{A_2}\] (as the side of the similar triangle is \[\dfrac{2}{3}\]of the corresponding sides of \[\Delta ABC\]) to the line AB such that it intersect AB at \[{B'}\] and is parallel to \[{A_3}B\].

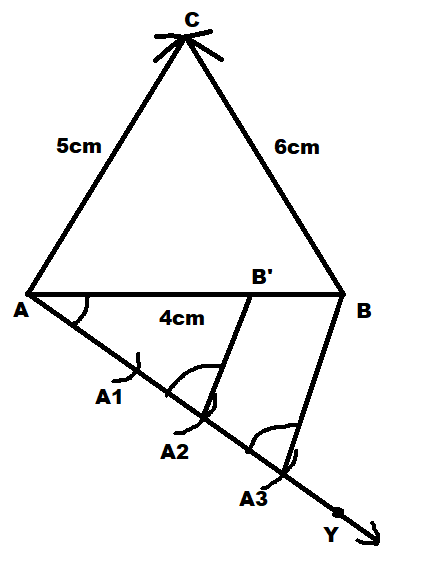
Now we will finally draw a line from \[{B'}\]to AC such that it intersects AC at \[{C'}\]and the line \[{B'}{C'}\]is parallel to the line BC.

Note:
Students should use the compass and scale for perfect measurement and arcs an accurate distance to get the desired triangles.
Also, we have drawn three arcs on the ray AY because we had to construct a similar triangle such that its sides are \[\dfrac{2}{3}\] of the corresponding sides of the first triangle.