Question

Construct an isosceles triangle whose altitude is 6.6 cm and the vertex angle is 60°.

Answer 1

Hint: Find the other two angles of the isosceles triangle. Then find the length of the sides of the triangle using the length of the altitude. Then construct the triangle with the sides and angles.

Complete step-by-step answer:
We are asked to construct an isosceles triangle whose altitude is 6.6 cm and the vertex angle is 60°.
We know that two angles of an isosceles triangle are equal. Let the equal angles be x.
The sum of the angles of a triangle is 180°. Then, we have:
\[60^\circ + x + x = 180^\circ \]
Solving for x, we have:
\[2x = 180^\circ - 60^\circ \]
\[2x = 120^\circ \]
\[x = \dfrac{{120^\circ }}{2}\]
\[x = 60^\circ \]
Hence, all three angles of the triangle are equal. Then, it is an equilateral triangle.
We know that the altitude of an equilateral triangle is also the angle bisector.
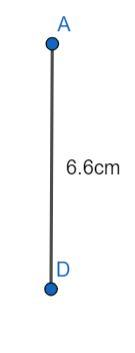
As the first step in construction, we draw a vertical line segment AD of length 6.6 cm.

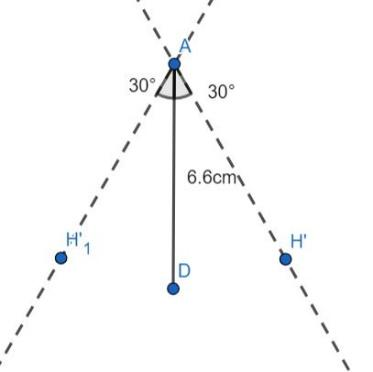
With A as the vertex, draw two lines making an angle of 30° with the line segment AD. Then, we have as follows:

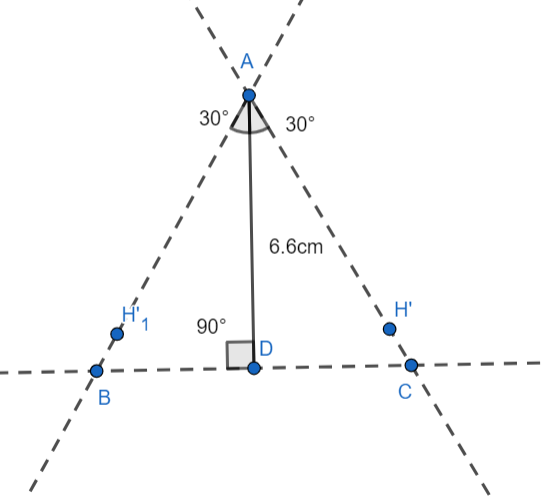
Now draw a perpendicular to the line segment AD that passes through point D, this line intersects the lines \[AH{'_1}\] and \[AH'\] at points B and C respectively.

Join the points A, B, and C.

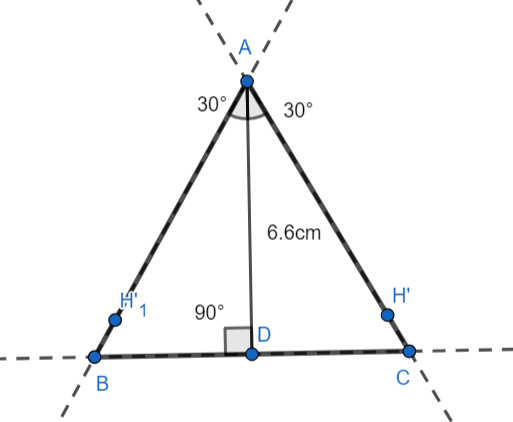
The triangle ABC is the required isosceles triangle with altitude 6.6 cm and the vertex angle 60°.

Note: We can also directly use the fact that the altitude to the base bisects the vertex angle of an isosceles triangle. It is not true for the equal angles of the isosceles triangle but it is true for all three angles of an equilateral triangle.