Question

CsBr crystallizes in a body-centered cubic lattice of unit cell edge length 436.6 pm. Atomic masses of Cs and Br are 133 amu and 80 amu respectively. The density ( in g/) of CsBr is:
A. 8.50
B. 4.25
C. 42.5
D. 0.425

Answer 1

Hint: From the unit cell dimensions we can calculate the density of the unit cell. We can calculate the density of the metal. knowing the mass of the atoms in the unit cell. Mass of a single atom gives an accurate determination of Avogadro’s constant ( )

Complete step by step solution:
Suppose the edge length of the unit cell is ‘a’, ‘d’ is the density of the metal and M is the molar mass. Volume of the unit cell is .
Mass of the unit cell is (number of atoms in unit cell*mass of each atom) =Z*m
Z is the number of atoms present in one unit cell, this is predicted by the type of lattice given in the question .We are given that the metal has bcc that is body centered unit cell . In this unit cell the same atoms are present in the corners and also at the centre of the unit cell as the name suggests which tells that the effective number of atoms (Z) =2. There are no atoms present anywhere else.

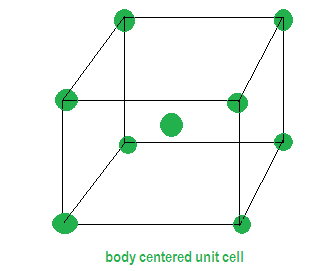
d= ? Z=2 a= 436.6pm edge length ${N_A} = 6.022 \times {10^{23}}$
Density of cubic unit cell =$\dfrac{{ZM}}{{{a^3}{N_A}}}$ 1 pm = ${10^{ - 10}}$ cm
$\Rightarrow \, d \, = \, \dfrac{{2 \times M}}{{{{(436.6 \times {{10}^{ - 10}})}^3} \times 6.022 \times {{10}^{23}}}}$
M or molecular weight of CsBr is given by adding the atomic mass unit of cesium and bromine which would be 133+80=213 amu. Now substituting the value of M in the formula above we get,
$d \,= \dfrac{{2 \times 213}}{{{{(436.6 \times {{10}^{ - 10}})}^3} \times 6.022 \times {{10}^{23}}}} = 8.5gc{m^{ - 3}}$
Hence we get the density of the unit cell.

Therefore the correct option is option A.

Note:
The effective number of atoms in FCC is (one from all the corners, 1 at the centre of the body of unit cell i.e.8*1/8 +1=2). Bcc is a type of bravais lattice.