Question

Cylinder A has a diameter of 7 cm, and the height is 14 cm, and cylinder B has a diameter of 14 cm, and the height is 7 cm. Without calculation, tell the volume of which cylinder is more? Verify the answer by calculation.

Answer 1

Hint: The cylinder is a three-dimensional shape with two round shapes at either end and has two parallel lines connecting the round ends. These two rounds shapes are the base of the cylinder and their center are joined by a line segment.
The volume of a 3-dimensional shape determines the capacity it can hold or the capacity it has, and in the case of a cylinder, it determines the capacity of the cylinder.
The volume of the cylinder is given as \[V = \pi {r^2}h\] where, (r) is the radius of the base.

Complete step-by-step answer:
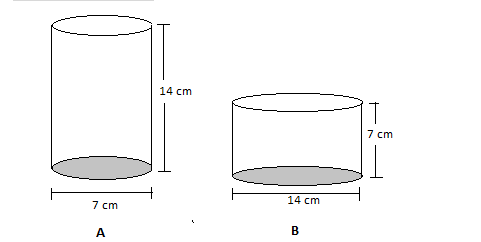
In this question, to determine which figure is bigger in terms of volume by checking the dimensions of both the figures and then finding and comparing the volume of each shape. To start with, we can see that the volume of the cylinder is proportional to the square of the radius of the base and height so, we can say that the volume majorly depends on the radius than the height of the cylinder.
The formula for the volume of a cylinder is given as \[V = \pi {r^2}h\]
It can be seen that volume is directly dependent on the square of the radius\[V \propto {r^2}\]and the radius of figure A \[\left( {{r_A} = \dfrac{d}{2} = \dfrac{7}{2} = 3.5} \right)\], and for figure B \[\left( {{r_B} = \dfrac{d}{2} = \dfrac{{14}}{2} = 7} \right)\], hence we can say the volume of figure B is greater than figure A.
Now, to verify our assumption we need to do calculation for the volume.
Substitute the value of radius and the height as 3.5 cm and 14 cm respectively in the formula \[V = \pi {r^2}h\] to calculate the volume of the figure A as:
\[
  {V_A} = \pi {r^2}h \\
   = \pi \times {\left( {\dfrac{7}{2}} \right)^2} \times 14 \\
   = \dfrac{{22}}{7} \times \dfrac{7}{2} \times \dfrac{7}{2} \times 14 \\
   = 11 \times 7 \times 7 \\
   = 539c{m^3} \\
 \]
Substitute the value of radius and the height as 7 cm and 3.5 cm respectively in the formula \[V = \pi {r^2}h\] to calculate the volume of the figure B as:
\[
  {V_B} = \pi {r^2}h \\
   = \pi \times {\left( {\dfrac{{14}}{2}} \right)^2} \times 7 \\
   = \dfrac{{22}}{7} \times 7 \times 7 \times 7 \\
   = 22 \times 7 \times 7 \\
   = 1078c{m^3} \\
 \]
As, $ {V_B} > {V_A} $ so, we can see the volume of figure B is more than figure A.

Note: To find the capacity of a closed curve/body, the volume is calculated for a three-dimensional object, and the area is calculated for a two-dimensional figure. It is interesting to note here that, every three-dimensional body is originated by rotating/revolving the two-dimensional body.