Question

Define Adjacent angles, Linear pair of angles. What is the sum of a linear pair of angles?

Answer 1

Hint: We start the problem by explaining what are adjacent angles, types of adjacent angles and properties of them. We then give examples which support the adjacent angles conditions. Similarly, we define what a linear pair of angles are and properties of them. We then prove the sum of the linear pair of angles as \[{{180}^{\circ }}\] by taking an example which clearly depicts a linear pair of angles.

Complete step-by-step answer:
In the question we are asked to define Adjacent angles, Linear pairs of angles. Then we have to tell what is the sum of a linear pair of angles.
After writing definitions of the term we will give a description about them also to give a clear picture about them.
Adjacent Angles: The two angles are said to be adjacent angles when they share the common vertex and side. The endpoints of the ray from the side of an angle is called the vertex of the angle. Adjacent angles can be a complementary angle (which sum up to ${{90}^{\circ }}$) or supplementary angle (which sum up to ${{180}^{\circ }}$) when they share the common vertex and side.
For example, let us consider a wall clock, the minute hand and second hand of a clock from one angle which shares a vertex and have common sides thus considered as adjacent angles.
Linear pair of angles: Pair of adjacent angles whose measures add up to form a straight angle is known as linear pair. The angles in a linear pair are supplementary.
Linear pair of angles is actually a special form of adjacent angles where only one condition is necessary that if sum up to ${{180}^{\circ }}$.
Suppose consider the figure,

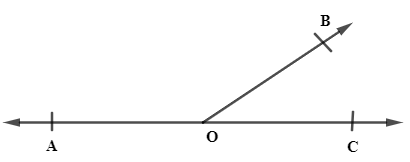
$\angle AOB+\angle BOC\ =\ {{180}^{\circ }}$ so here, $\angle AOB$ and $\angle BOC$ is adjacent as well as linear pair as their sum adds up to ${{180}^{\circ }}$.

Note: We should not confuse adjacent angles with the linear pair of angles. We can solve the interior and exterior angles in the polygons by using the concept of linear pair of angles. We can see most of the problems involving parallel lines and transversal lines can be solved by using the concept of adjacent and linear pairs of angles.