Question

Define Critical angle and also find formula for the critical angle.

Answer 1

Hint: The above problem can be resolved using the concepts and the fundamentals of the refractive index as well as the critical angle. The Critical angle is that value of angle at which the refraction takes place in perpendicular direction. There are several applications of the critical angle, but the primary application of the critical angle is to determine the phenomenon of Total Internal Reflection.

Complete step by step answer:
When a light ray travels in a medium, strikes a surface such that there is some reflection occurring from the surface. And the incident ray of light will form a specific angle of incidence, this specific angle of incidence is that value of angle of incidence, beyond which the phenomena of total internal reflection can happen to take place.
Let us consider two mediums of different values of index. If \[{i_C}\] be the value of critical angle

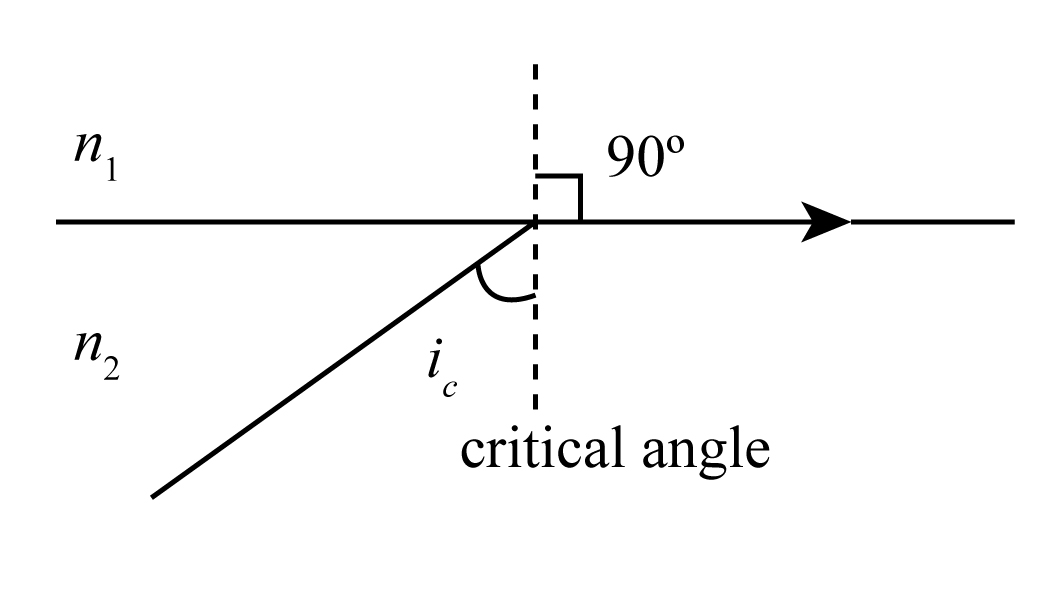
Here, \[{n_1}\] is the refractive index of one medium and \[{n_2}\]is the refractive index of another medium.
Then apply the Snell’s law as,
\[{n_1}\sin {\theta _1} = {n_2}\sin {\theta _2}\]……………………………..(1)
Here, \[{\theta _1}\] is the angle of incidence and \[{\theta _2}\] is the angle of refraction.
As, for the condition of critical angle, the refraction angle is at perpendicular direction.
Then substituting the value of \[{\theta _2}\] in equation 1 as,
\[\begin{array}{l}
{n_1}\sin {\theta _1} = {n_2}\sin {\theta _2}\\
\Rightarrow {n_1}\sin {i_C} = {n_2}\sin 90\;^\circ \\
\Rightarrow \sin {i_C} = \dfrac{{{n_2}}}{{{n_1}}}\\
\Rightarrow {i_c} = {\sin ^{ - 1}}\left( {\dfrac{{{n_2}}}{{{n_1}}}} \right)
\end{array}\]

Note:To solve the given problem, one must be aware of the phenomenon used in optics like refractions, reflection, angle of refraction, critical angle and many more. These variables have a direct impact on the angle of inclinations, namely called the angle of incidence and the angle of refraction. Moreover, one must remember the mathematical relations as per Snell's Law and their relations with the refractive indices of media.