Question

Define lateral displacement of light. Give the formula to find the refractive index of the glass slab in terms of angle of incidence and angle of refraction.

Answer 1

Hint: When a beam of light encounters another transparent medium, a part of the light gets reflected back into the first medium while the rest enters the other. When it enters into the other medium it changes the direction of its path. This phenomenon is called refraction. A refractive index is a constant number for a particular medium. Refractive index is defined as the ratio of the sine of the angle of the incidence to the sine of the angle of refraction.

Complete step by step solution:
Step 1: Definition of lateral displacement- lateral displacement is the perpendicular distance between the incident ray and the emergent ray. Let us understand what happens when light enters in a different medium.

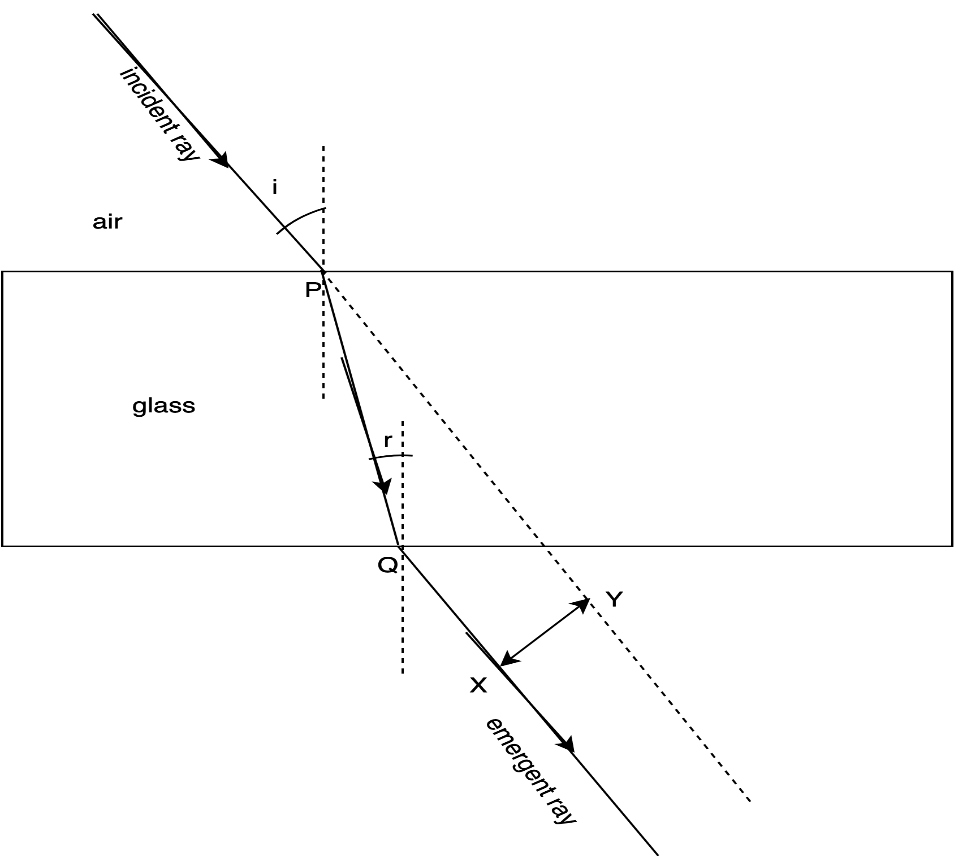
In the above diagram, an incident ray enters from air to glass. At point P the ray is refracted by the glass and changes its path. When the ray enters the air from the glass at point Q it gets refracted again and travels in the same direction as the incident ray. The distance between the two lines is XY. This distance is called the lateral displacement.
Step 2: For the formula of refractive index first we will see Snell’s law of refraction. The law states that, 1. The incident ray, the refracted ray, and the normal to the interface at the point of incidence, all lie in the same plane, and 2. The ratio of the sine of the angle of incidence to the sine of the angle of refraction is constant. Remember that the angles of incidence $i$ and refraction $r$ are the angles that the incident and its refracted ray make with the normal, respectively.
Therefore we have,
$\therefore \dfrac{{\sin i}}{{\sin r}} = {n_g}$ , where ${n_g}$ is the refractive index of the glass slab. A refractive index is a constant number. For example, the refractive index for air is always 1.

Note: Refraction should not be confused with reflection. Both are entirely different concepts. Refractive index is a relative term which means that when we say that the refractive index of the glass is ${n_g}$ , the refractive index is with respect to another medium. In the above example, the refractive index of glass is with respect to air.