Question

Describe the astronomical telescope on the basis of the following points:
(i) Labelled ray diagram.
(ii) Derivation of formula for magnifying power, when the final image is formed at the least distance of distinct vision.

Answer 1

Hint: Telescope is used to observe objects which are very far from us. Telescopes produce magnified images of distant objects. In a simple telescope two lenses are used, objective lens and eyepiece lens. A parallel beam of light is focused by the objective lens of a telescope and then light passes through an eyepiece forming a magnified image.

Complete step by step answer:

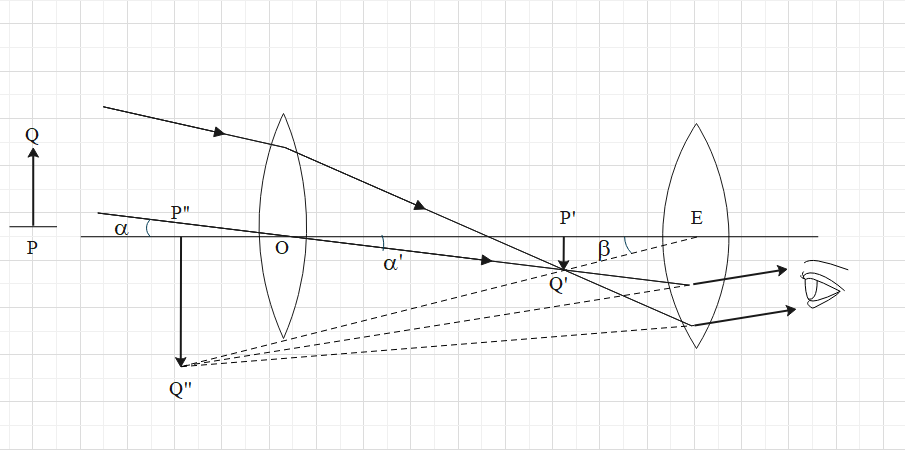
It consists of two converging lenses placed coaxially. The one facing the distant object is called the objective and has a large aperture and a large focal length. The other is called the eyepiece, as the eye is placed close to it. It has a smaller aperture and a smaller focal length. The lenses are fixed in tubes. The eyepiece tube can slide within the objective tube so that the separation between the objective and the eyepiece may be changed.
When the telescope is directed towards a distant object\[PQ\], the objective forms a real image of the object in its focal plane. If the point P is on the principal axis, the image point $P$ is at the second focus of the objective. The rays coming from $Q$ are focused at$Q'$. The eyepiece forms a magnified virtual image \[P''Q''\]of\[P'Q'\]. This image is finally seen by the eye. In normal adjustment, the position is so adjusted that the final image is formed at infinity. In such a case, the first image \[P'Q'\] is formed in the first focal plane of the eyepiece. The eye is least strained to focus this final image. The image can be brought closer by pushing the eyepiece closer to the first image. Maximum angular magnification is produced when the final image is formed at the near point.
Suppose, the objective and the eyepiece have focal lengths ${{f}_{o}}$and${{f}_{e}}$ respectively and the object is situated at a large distance ${{u}_{0}}$ from the objective. The object \[PQ\] in figure subtends an angle $\alpha $ on the objective. Since the object is far away, the angle it would subtend on the eye, if there were no telescope, is also essentially$\alpha $.
As${{u}_{0}}$ is very large, the first image\[P'Q'\] is formed in the focal plane of the objective.
From the figure,
$\left| \alpha \right|=\left| \alpha ' \right|\approx \left| \tan \alpha ' \right|=\dfrac{P'Q'}{OP'}=\dfrac{P'Q'}{{{f}_{0}}}---(1)$
The final image \[P''Q''\]subtends an angle$\beta $on the eyepiece. We have, from the $\vartriangle P'Q'E$
$\left| \beta \right|\approx \left| \tan \beta \right|=\dfrac{P'Q'}{EP'}---(2)$
\[\text{From }\left( \text{1} \right)\text{ }\!\!~\!\!\text{ and }\left( \text{2} \right)\]
$\left| \dfrac{\beta }{\alpha } \right|=\dfrac{{{f}_{0}}}{E'P'}$
If the telescope is set for normal adjustment so that the final image is formed at infinity, the first image \[P'Q'\] must be in the focal plane of the eyepiece. Then\[E'P'\text{ }=\text{ }{{f}_{e}}\].
$\left| \dfrac{\beta }{\alpha } \right|=\dfrac{{{f}_{0}}}{{{f}_{e}}}$
The angular magnification or the magnifying power of the telescope is defined as
\[\text{m=}\dfrac{\text{angle subtended by the final image on the eye m}}{angle\text{ subtended by the object on the unaided eye}}\]
The angles$\beta $ and $\alpha $ are formed on the opposite sides of the axis. Hence, their signs are opposite and $\dfrac{\beta }{\alpha }$is negative. Thus,
$m=\dfrac{\beta }{\alpha }=-\left| \dfrac{\beta }{\alpha } \right|$
$m=-\dfrac{{{f}_{0}}}{{{f}_{e}}}$
If the telescope is adjusted so that the final image is formed at the near point of the eye, the angular magnification is further increased. Let us apply the lens equation to the eyepiece in this case.
\[\text{Here u = E }\!\!'\!\!\text{ P }\!\!'\!\!\text{ and v = -E }\!\!'\!\!\text{ P }\!\!'\!\!\text{ = -D}\]
The lens equation is
$\begin{align}
  & \dfrac{1}{v}-\dfrac{1}{u}=\dfrac{1}{f} \\
 & \dfrac{1}{-D}-\dfrac{1}{-E'P'}=\dfrac{1}{{{f}_{e}}} \\
\end{align}$
$\dfrac{1}{E'P'}=\dfrac{1}{{{f}_{e}}}+\dfrac{1}{D}=\dfrac{{{f}_{e}}+D}{{{f}_{e}}D}$
By (2)
$\left| \dfrac{\beta }{\alpha } \right|=\dfrac{{{f}_{o}}({{f}_{e}}+D)}{{{f}_{e}}D}$
The magnification is
$m=\dfrac{\beta }{\alpha }=-\left| \dfrac{\beta }{\alpha } \right|=\dfrac{{{f}_{o}}({{f}_{e}}+D)}{{{f}_{e}}D}=-\dfrac{{{f}_{o}}}{{{f}_{e}}}\left( 1+\dfrac{{{f}_{e}}}{D} \right)$

Note: In order to have a larger magnification of the telescope focal length of the objective should be as large as practically possible and the focal length of the eyepiece should be as small as possible. The image is formed at infinity in normal adjustment. Both lenses should be the converging lens. Image of an object is always inverted with respect to the object formed by an astronomical telescope. We all know that heavenly bodies are usually spherical in shape therefore it does not matter whether the image formed by an astronomical telescope is inverted or not.