Question

How do you determine if $\cos 35^\circ \, < \cos 45^\circ \,$ is true or false?

Answer 1

Hint: In trigonometry $\cos $ is a primary function as $\sin $ and can be defined as the ratio between the base of a right- angled triangle and the hypotenuse of the right-angled triangle. A right- angled triangle is the one that has equal to $90^\circ $. The $\cos $ of different angles has their specific values which are important in solving various trigonometric problems.

Complete step by step answer:
In basic trigonometry, $\cos $ deals with various operations with the right- angled triangle. In right- angled there are different notations according to the relation of each line segment of the triangle and its relation with the other and they have specific names such as the opposite (height of the triangle), Adjacent (base of the triangle) and hypotenuse (the line joining the tip of the base and the height).
The relations of these line segments of the triangle are expressed with three specific functions known as Sine, Cosine and Tangent.
Now, we consider a right triangle, the angle made by the base and hypotenuse will be considered as $\theta $ and in case of the cosine function, the angle between the adjacent and hypotenuse is only taken into account.
Therefore, $\cos \theta = \dfrac{{Base}}{{Hypotenuse}}$
Here, in this question we have to determine whether $\cos 35^\circ \, < \cos 45^\circ \,$ is true or false. For this we will check that the cosine function is a decreasing function or increasing function.
So, let us consider a right- triangle angle where the angle made by the base and hypotenuse $\theta $.

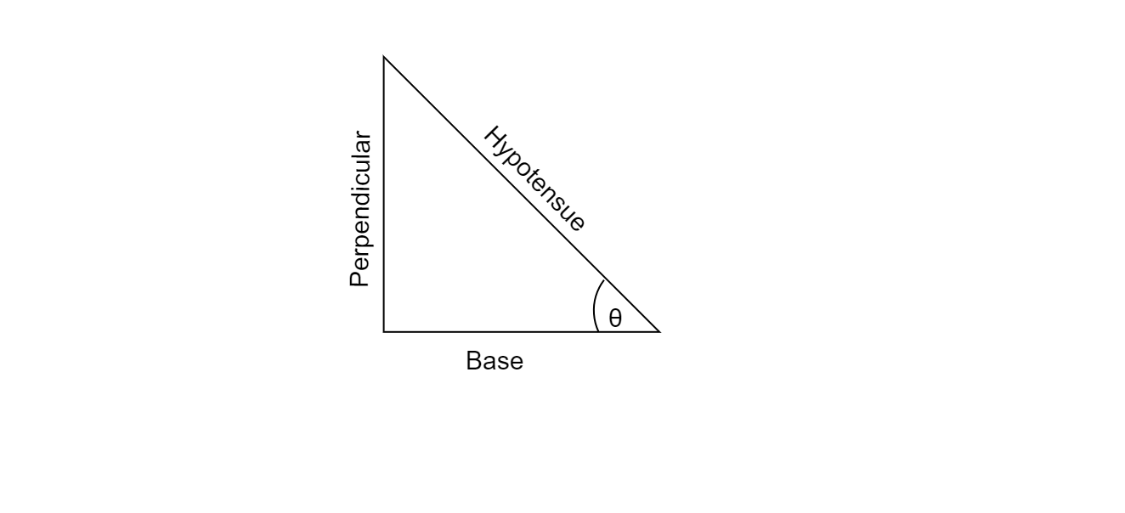
Now, if we increase the angle $\theta $, and keep the hypotenuse same then the adjacent side (base) continues to reduce and when $\theta $ becomes $90^\circ $, the adjacent side reduces to $0$.

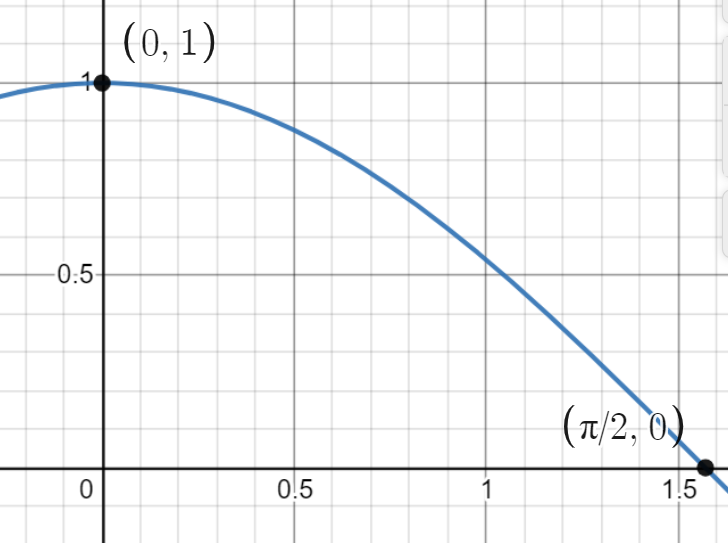
Therefore, cosine is a decreasing function and it is also clear from the values of cosine angles i.e., $\cos 0^\circ = 1$ and $\cos 90^\circ = 0$. The value of cosine function decreases on increasing the value of angles.
Hence, the given statement is False.
The correct statement will be $\cos 35^\circ \, > \cos 45^\circ \,$.

Note:
Trigonometric functions also known as circular functions are the functions or ratios which state the relationship between the angles and side of the right- angled triangle. The basic trigonometric functions are sine, cosine, tangent, secant, cosecant and cotangent. In these trigonometric functions $\sin ,\,\tan ,\,\sec $ are increasing functions whereas $\cos ,\,\csc ,\cot $ are decreasing functions.