Question

Determine the electric dipole moment of the system of three charges, placed on the vertices of an equilateral triangle, as shown in the figure:

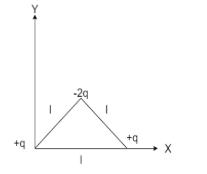
A) $(ql)\dfrac{{\widehat i + \widehat j}}{{\sqrt 2 }}$
B) $\sqrt 3 ql\dfrac{{\widehat j - \widehat i}}{{\sqrt 2 }}$
C) $ - \sqrt 3 ql\widehat j$
D) $2ql\widehat j$

Answer 1

Hint:Recall that the electric dipole is nothing but two equal and opposite charges separated by a small distance. If two charges that are equal in magnitude but opposite in direction are separated by a distance then they form a dipole.

Complete step by step answer:
Step I:
The charge $ - 2q$ can be written as $ - q - q$
This is because a dipole is formed by opposite charges. Here two dipoles are formed by using charges $ - q$ and $ + q$

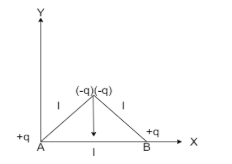
Step II:

The net dipole moment will act as a long negative Y-axis. The formula for dipole moment is mathematically written as

$P = q.d$

Where ‘q’ is the magnitude of opposite charges
And ‘d’ is the distance between charges.
In this case, the distance is ‘l’.

Step III:
Since the charges are placed at the corners of an equilateral triangle, so the angle formed by each side of the equilateral triangle is ${60^ \circ }$. The dipole moment across point A is written as

${P_1} = q.l\cos {30^ \circ }$

Similarly, the dipole moment at point B is written as

${P_2} = q.l\cos {30^ \circ }$

Step IV:
The sine components act in opposite directions and hence cancel each other. So, the resultant dipole can be written as

${P_R} = 2ql\cos {30^ \circ }$
${P_R} = 2ql.\dfrac{{\sqrt 3 }}{2}$
${P_R} = \sqrt 3 ql$

Since the net dipole moment is formed in the negative Y-axis, so it can be written as

${P_R} = - \sqrt 3 ql\widehat j$

Step V:

$ \Rightarrow $Option C is the right answer.

Note:It is to be remembered that the term dipole and dipole moment are different and not the same. An electric dipole moment is the product of the magnitude of two charges and the distance of separation between them. Its direction is from negative charge to positive charge.