Question

How can you determine the focal length of a convex lens experimentally? Draw a rough diagram.

Answer 1

Hint – You can start by describing the equipment required for this experiment, i.e. optical bench. Then discuss the method of taking measurement using the optical bench. Use the data obtained to find out the focal length of the combination of lenses by using the lens formula, i.e. $\dfrac{1}{f} = \dfrac{1}{v} - \dfrac{1}{u}$. Then use the equation for the focal length of the convex lens and concave lens in contact, i.e. $\dfrac{1}{f} = \dfrac{1}{{{f_1}}} + \dfrac{1}{{ - {f_2}}}$ to find out the focal length of the convex lens.

Step By Step Answer:
For performing this experiment, you would need an optical bench. An optical bench is a wooden flat rectangular board that has a metal rod installed on it. On the metal rod, holders (generally made out of metal) are installed. The holders can slide freely on the metal rod. Holders on the free end attach to lenses (convex or concave) or to pointer needles.

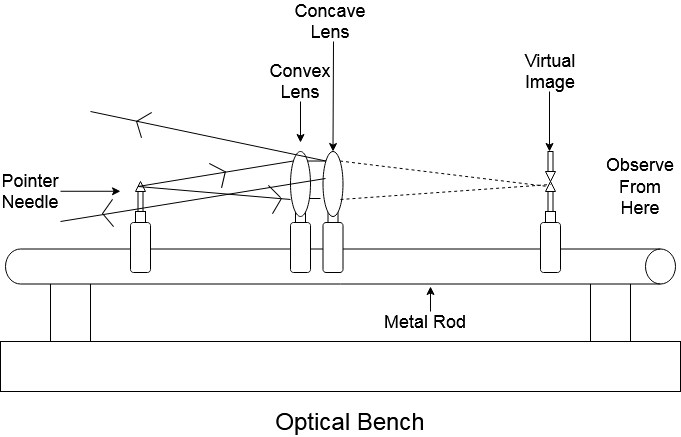
Now, to find out the focus length of the convex lens, we need a concave lens of known focal length and two pointer needles one at each side of the combination of the lenses(refer to diagram). Keep the lenses in contact with each other. Now, we use the concept of a combination of thin lenses in contact. Let ${f_1}$ ,${f_2}$ and ${f_T}$ be the focal length of the convex lens, the concave lens and the focal length of the combination of lenses respectively.

Before finding the focal length, follow these steps –

1.)Look at the concave lens, while keeping the 2nd pointer needle in the line of sight(refer to diagram)

2.)Now, adjust both the pointer needles in such a way that you see a perfectly clear virtual image of the 1st pointer needle over the 2nd pointer needle.

3.)Note down the distance of 1st and 2nd pointer needle from the center of the combination of lenses(i.e. $u$ and $v$ respectively)

By lens formula we have

$\dfrac{1}{f} = \dfrac{1}{v} - \dfrac{1}{u}$
$ \Rightarrow \dfrac{1}{{{f_T}}} = \dfrac{1}{v} - \dfrac{1}{u}$(Equation 1)
Calculate the values of ${f_T}$ by substituting the value of $v$ and $u$. $ \Rightarrow \dfrac{1}{{{f_T}}} = \dfrac{1}{{{f_1}}} - \dfrac{1}{{{f_2}}}$

We know for a convex lens and concave lens in contact,

$\dfrac{1}{f} = \dfrac{1}{{{f_1}}} + \dfrac{1}{{ - {f_2}}}$

$ \Rightarrow \dfrac{1}{{{f_1}}} = \dfrac{1}{{{f_T}}} + \dfrac{1}{{{f_2}}}$
$ \Rightarrow {f_1} = \dfrac{{{f_T}{f_2}}}{{{f_T} + {f_2}}}$

Since we already calculated the value of ${f_T}$ and the value of ${f_2}$ is already known, we can easily calculate the value of the focal length of the convex length.

Note – This method can also be used to calculate the focal length of a convex lens by using another convex lens of known focal length, or for calculating the focal length of concave lenses by using convex or concave lenses of known focal length. To use the concept of combination of lenses in contact, it is necessary that both lenses are as thin as possible.