
How many diagonals does a convex quadrilateral have?
[a] 1
[b] 2
[c] 3
[d] 4
Answer
522.3k+ views
3 likes
Hint: Recall that a diagonal is a line segment formed by two points of a polygon such that the points are not connected by the side of the polygon. Use the definition of a convex polygon and think how many diagonals can a convex quadrilateral have.
Complete step-by-step answer:
We know that a diagonal of a polygon is a line segment formed by joining two points of the polygon which are not connected by the side of the polygon.
A convex polygon is a polygon having the following property:
If any two points A and B are inside the polygon, then the whole line segment AB is inside the polygon. Hence a convex quadrilateral has all angles smaller than
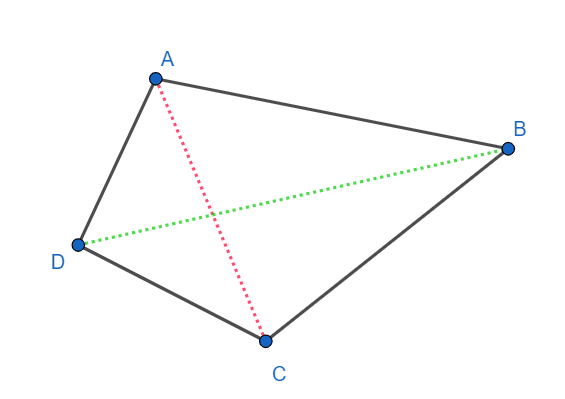
ABCD is an example of a convex quadrilateral. It is clear from the picture that only the pairs of point (A, C) and (B, D) are not connected by a side.
Hence ABCD has two diagonals AC and BD.
Hence a convex quadrilateral has 2 diagonals.
Hence option [b] is correct.
Note: Alternatively, we know that the number of diagonals in a polygon of n sides is given by
Put n= 4, we get
The number of diagonals in a quadrilateral
Hence option [b] is correct.
Complete step-by-step answer:
We know that a diagonal of a polygon is a line segment formed by joining two points of the polygon which are not connected by the side of the polygon.
A convex polygon is a polygon having the following property:
If any two points A and B are inside the polygon, then the whole line segment AB is inside the polygon. Hence a convex quadrilateral has all angles smaller than

ABCD is an example of a convex quadrilateral. It is clear from the picture that only the pairs of point (A, C) and (B, D) are not connected by a side.
Hence ABCD has two diagonals AC and BD.
Hence a convex quadrilateral has 2 diagonals.
Hence option [b] is correct.
Note: Alternatively, we know that the number of diagonals in a polygon of n sides is given by
Put n= 4, we get
The number of diagonals in a quadrilateral
Hence option [b] is correct.
Recently Updated Pages
Express the following as a fraction and simplify a class 7 maths CBSE

The length and width of a rectangle are in ratio of class 7 maths CBSE

The ratio of the income to the expenditure of a family class 7 maths CBSE

How do you write 025 million in scientific notatio class 7 maths CBSE

How do you convert 295 meters per second to kilometers class 7 maths CBSE

Write the following in Roman numerals 25819 class 7 maths CBSE

Trending doubts
A boat goes 24 km upstream and 28 km downstream in class 10 maths CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

What are the public facilities provided by the government? Also explain each facility

Difference between mass and weight class 10 physics CBSE

SI unit of electrical energy is A Joule B Kilowatt class 10 physics CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE




