Question

How does distance affect magnetic force ?

Answer 1

Hint:Coulomb's Inverse Square Law of Magnetic Force, also known as Coulomb's Law of Magnetic Force, was introduced in \[1785\] by Charles-Augustin de Coulomb, a French physicist and military engineer. For two isolated point poles, he interpreted the quantitative expression of power.

Complete answer:
The force of attraction or repulsion between two magnetic poles of strengths \[{m_1}\] and \[{m_2}\] held at a distance r apart is directly proportional to the product of their pole strengths and inversely proportional to the square of the distance between them.
$F \propto \dfrac{{{m_1}{m_2}}}{{{r^2}}}$ or $F = \dfrac{{{\mu _o}}}{{4\pi }}\dfrac{{{m_1}{m_2}}}{{{r^2}}}$

Any scientific law stating that a given physical quantity is inversely proportional to the square of the distance from the source of that physical quantity is known as an inverse-square law.With respect to distance, magnetic force follows an inverse square law. The magnetic force equation is identical to Coulomb's law (if you are familiar with it). The important thing to remember is that force is inversely proportional to distance squared (i.e. it obeys an inverse square law with distance).
$F \propto \dfrac{1}{{{r^2}}}$
Where $r$ is the distance between the magnets.

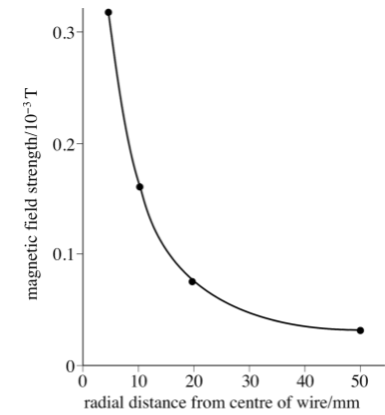
Note:A unit magnetic pole is known as a magnetic pole that experiences a force of \[1/2r\] newtons when placed one metre away from a very long straight conductor carrying a current of one ampere.