
Draw a circle of diameter 9 cm. Mark a point at a distance of 7.5 cm from the center of the circle. Draw tangents to the given circle from this exterior point. Measure the length of each tangent.
Answer
508.2k+ views
Hint: To solve this first we have to write the steps of construction and then draw the figures with respective dimensions. Draw a circle of radius 4.5 and now draw a line from center and from the end point of line draw tangents and now measure the distance.
Given: Diameter = 9cm
Radius =
Complete step-by-step answer:
Mark a point O. Draw a circle of radius 4.5cm.
From the point mark a point P such OP = 7.5cm
Draw tangents PT and PR from the point P such that it touches the circumference of the circle.
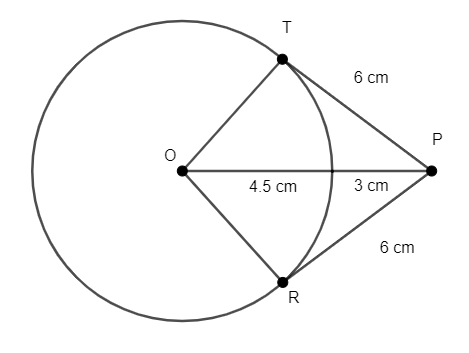
From the diagram we can see that a right angled triangle is formed by OTP.
Now by Pythagoras theorem we can find the distance from point P to R which is a tangent to a circle.
t is the distance from P to R.
Length of the tangents PT = 6cm and PR = 6 cm.
Note: The right angle is at vertex T. There are two tangents drawn from a point and they have the same distance if they are projected on a circle. The tangents are the lines which just touch the circle. All dimensions are in cm.
Given: Diameter = 9cm
Radius =
Complete step-by-step answer:
Mark a point O. Draw a circle of radius 4.5cm.
From the point mark a point P such OP = 7.5cm
Draw tangents PT and PR from the point P such that it touches the circumference of the circle.

From the diagram we can see that a right angled triangle is formed by OTP.
Now by Pythagoras theorem we can find the distance from point P to R which is a tangent to a circle.
t is the distance from P to R.
Length of the tangents PT = 6cm and PR = 6 cm.
Note: The right angle is at vertex T. There are two tangents drawn from a point and they have the same distance if they are projected on a circle. The tangents are the lines which just touch the circle. All dimensions are in cm.
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Questions & Answers - Ask your doubts

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 Science: Engaging Questions & Answers for Success

Trending doubts
Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Difference Between Plant Cell and Animal Cell

Given that HCF 306 657 9 find the LCM 306 657 class 9 maths CBSE

The highest mountain peak in India is A Kanchenjunga class 9 social science CBSE

What is pollution? How many types of pollution? Define it

Differentiate between the Western and the Eastern class 9 social science CBSE




