Question

Draw a heptagon. The number of diagonals emerging from one of the vertices is
A) 1
B) 2
C) 3
D) 4

Answer 1

Hint: Diagonal join to all other points in a figure other than the adjacent points.
First, we are going to draw a heptagon, then we are going to consider one of the points from the heptagon. Then we are going to draw the diagonals from that point and find out all the possible diagonals as required in the question.

Complete step by step solution:
Heptagon is a polygon (a closed shape made up of line segments) made up of 7 sides and 7 angles. The word heptagon is made up of two words, hepta meaning seven and gon meaning sides.
First, we are going to draw the heptagon

Now, we are going to consider one point from the heptagon and draw lines to a point other than the adjacent points. Diagonals are formed with all points other than adjacent sides.

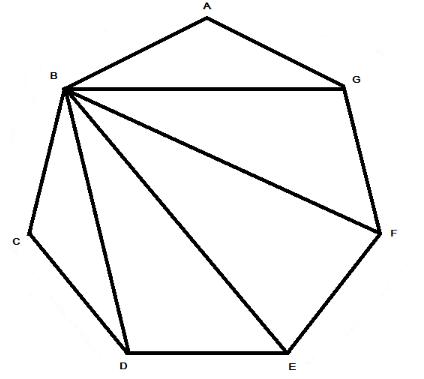
Similarly, we are going to do this to all non-adjacent points/vertices. Then we get after drawing
From the above drawn diagram, we can say that from one vertex of the heptagon, we can draw only 4 diagonals.

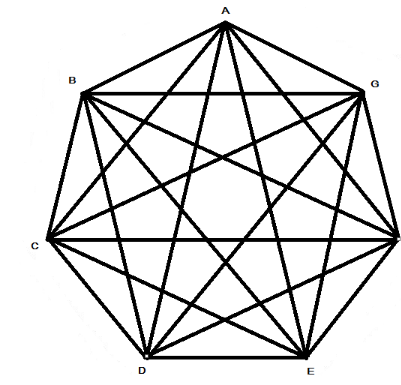
And totally we can have 14 diagonals in the heptagon on mapping the diagonals from each and every point of the heptagon. Which looks like this
So, the correct answer is “Option D”.

Note: Diagonals are the lines that can only be formed by vertices which are not adjacent to each and other and also diagonals can be found with the help of a formula of $\dfrac{{n(n - 3)}}{2}$, where n is the number of sides of a polygon.