Question

Draw a line segment AB of length 10 cm. Mark a point P on AB such that AP = 4 cm. Draw a line through P perpendicular to AB.

Answer 1

Hint: First of all, draw a line AB = 10 cm and mark point P such that AP = 4 cm. Now mark two points on both sides of P on line AB equidistant from P. Now with the centers at these points, draw an arc above line AB and proceed to get the required perpendicular.

Complete step-by-step answer:
Here, we have to draw a line segment AB of length 10 cm. Then, we have to mark a point P on AB such that AP = 4 cm. Finally, we have to draw a line through P which would be perpendicular to AB.
(i) Let us first draw the line AB = 10 cm with the help of a ruler as follows:

(ii) Now, with A as the center and 4 cm as the radius, we will draw an arc on AB as

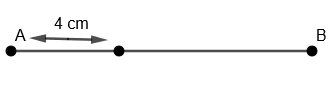
(iii) We will name this point as P such that AP = 4 cm.

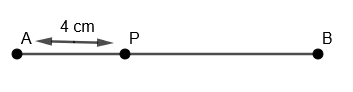
(iv) Now, we will take any radius, say 3 cm. With P as center and radius = 3 cm. We will draw an arc on the left side of P on line AB as,

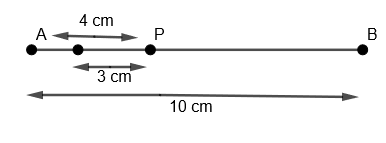
(v) We will name this as point C.

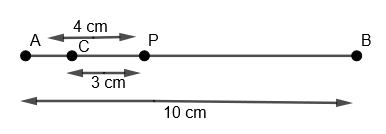
(vi) Now with the same radius that is 3 cm and with P as the center, we will again draw an arc on the right side of P on the line AB as,

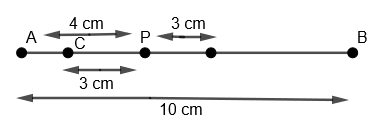
(vii) We will name this as point D.

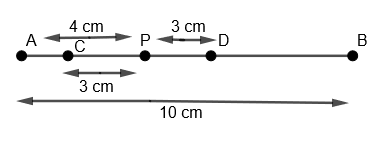
(viii) Now with D as center and radius greater than DP, we will draw an arc above line AB as,

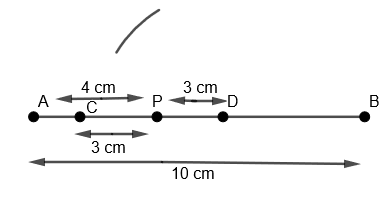
(ix) Now with C as the center and with the same radius as that of the previous step, we will draw an arc cutting the previous arc and we will name this point of intersection of two arcs as O.

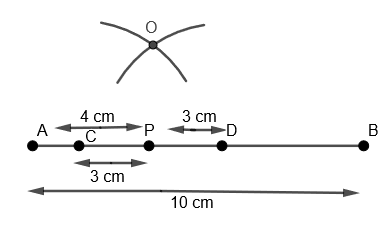
(x) Now we will join OP and extend it.

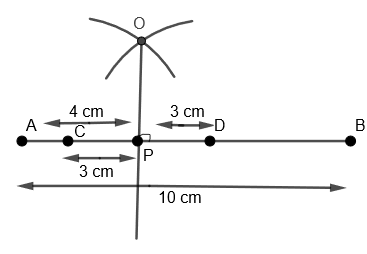
Hence, we get OP as the required perpendicular on line AB through P.

Note: Some students make this mistake of constructing the perpendicular bisector of AB but they must keep in mind that they have to construct perpendicular passing through P. Also, students can cross-check their construction by measuring if angle \[\angle OPD\] is \[{{90}^{o}}\] or not.