
Draw a pair of vertically opposite angles. Bisect each of the two angles. Verify that the bisecting rays are in the same line.
Answer
504.6k+ views
Hint- Here we need to do simple construction steps for drawing the required pair of vertical opposite angles which we will see later step wise. Then we will divide it with the help of compasses .Also we have to prove for the three joining points are in the straight line .For that purpose we need to find the sum of all angle along one side of the line if it come out to be equal to
Complete step-by-step solution -
The steps of construction are:
First draw two lines AB and CD intersecting at point O.
Taking O as center draw an arc cutting OA and OC at point P and Q respectively
Now taking P as center draw an arc whose radius is more than half of PQ and with the same radius and center Q draw an arc intersecting the previous arc at point M
Now join the point OM and produce it form a ray OX and therefore OX bisects angle AOC
Repeat the same steps as above to draw the angle bisector OY of angle BOD
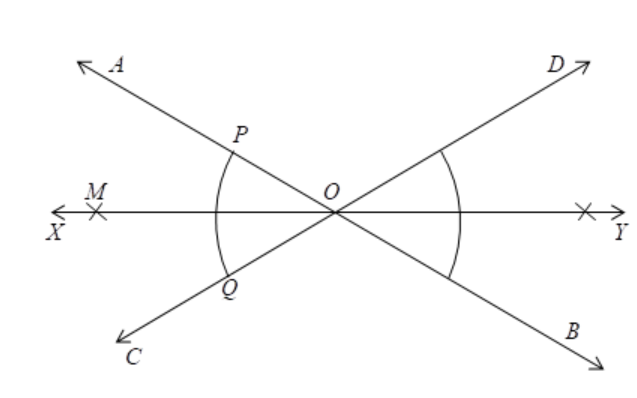
Now we will prove that XOY is a straight line
Since we know that
Therefore,
As from the construction OY is bisector of
Therefore,
Also, from the construction OX is bisector of
Therefore,
From equation (1)
Now divide both sides by 2
As we know that the angle bisector bisect the angles into two equal halves
Therefore,
As we know that the sum of linear pair angles is 180 degree
Therefore,
Since,
OX and OY are the two opposite rays of the same line. Hence, XOY is a straight line.
Note- In order to solve these types of questions, learn about the concept to draw angle bisectors and how to use compass and protractor to measure and draw angles. In order to prove the second part of the questions we use basic angle properties of the line such as linear pair, vertically opposite angles etc. You need to have concepts about corresponding angles, alternate angles etc. to solve questions of these types.
Complete step-by-step solution -
The steps of construction are:
First draw two lines AB and CD intersecting at point O.
Taking O as center draw an arc cutting OA and OC at point P and Q respectively
Now taking P as center draw an arc whose radius is more than half of PQ and with the same radius and center Q draw an arc intersecting the previous arc at point M
Now join the point OM and produce it form a ray OX and therefore OX bisects angle AOC
Repeat the same steps as above to draw the angle bisector OY of angle BOD

Now we will prove that XOY is a straight line
Since we know that
Therefore,
As from the construction OY is bisector of
Therefore,
Also, from the construction OX is bisector of
Therefore,
From equation (1)
Now divide both sides by 2
As we know that the angle bisector bisect the angles into two equal halves
Therefore,
As we know that the sum of linear pair angles is 180 degree
Therefore,
Since,
OX and OY are the two opposite rays of the same line. Hence, XOY is a straight line.
Note- In order to solve these types of questions, learn about the concept to draw angle bisectors and how to use compass and protractor to measure and draw angles. In order to prove the second part of the questions we use basic angle properties of the line such as linear pair, vertically opposite angles etc. You need to have concepts about corresponding angles, alternate angles etc. to solve questions of these types.
Latest Vedantu courses for you
Grade 11 Science PCM | CBSE | SCHOOL | English
CBSE (2025-26)
School Full course for CBSE students
₹41,848 per year
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Difference Between Plant Cell and Animal Cell

Given that HCF 306 657 9 find the LCM 306 657 class 9 maths CBSE

The highest mountain peak in India is A Kanchenjunga class 9 social science CBSE

What is the difference between Atleast and Atmost in class 9 maths CBSE

What is pollution? How many types of pollution? Define it




