Question

Draw a ray diagram for a concave mirror and prove that focal length of the mirror is half of its radius of curvature. Write a mirror equation for a concave mirror. When light enters from rarer to denser medium, what effect occurs on the values of wavelength and frequency of it?

Answer 1

Hint: Draw the ray diagram for the concave mirror and use the law of alternate angles and Snell’s law. Recall the mirror equation for the concave mirror. Use the relation between the velocity, frequency and wavelength to determine the effect of change of medium by the light.

Complete step by step answer:
The ray diagram for a concave mirror is as follows:

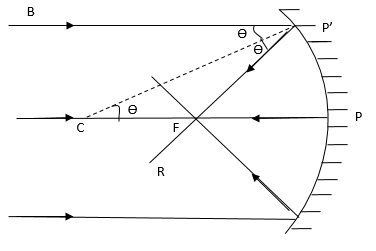
In the above ray diagram, PC is the principle axis, point F is the focus, Point C is the centre of curvature, the distance PF is the focal length of the concave mirror and the distance PC is the radius of curvature of the concave mirror.
The ray BP’ is incident on the concave mirror which is parallel to the principal axis PC and P’ is the point of incidence of the ray BP’. P’C is the normal to the concave mirror. The ray BP’ gets reflected from the concave mirror and passes through the focus of the mirror. After reflection, the incident ray passes along P’R.
The angles BP’C and P’CF are alternate angles. Hence, they are equal.
\[\angle {\text{BP'C}} = \angle {\text{P'CF}}\]
According to Snell’s law, the angle of incidence and the angle of reflection are always equal.
Hence, the angles BP’C (angle of incidence) and CP’F (angle of reflection) are equal to \[\theta \].
\[\angle {\text{BP'C}} = \angle {\text{CP'F}} = \theta \]
From the above two equations, one can conclude that the angles P’CF and BP’C must be equal.
\[\angle {\text{P'CF}} = \angle {\text{CP'F}}\]
If the adjacent angles of a triangle are equal, then the triangle is an isosceles triangle. The sides of the triangle opposite to the equal angles are also equal.
Hence, the triangle FP’C is an isosceles triangle and the sides P’F and FC of the triangle are equal.
\[{\text{P'F}} = {\text{FC}}\]
Also the aperture of the concave mirror is very small. Hence, the points P and P’ are very close to each other.
Hence, we can assume that the distances P’F and PF are approximately equal.
\[{\text{P'F}} = {\text{PF}}\]
From the above two relations of distance, we can write
\[{\text{FC}} = {\text{PF}}\]
The distance PC is the sum of the distances FC and PF.
\[{\text{PC}} = {\text{PF}} + {\text{FC}}\]
Substitute \[{\text{PF}}\] for \[{\text{FC}}\] in the above equation.
\[{\text{PC}} = {\text{PF}} + {\text{PF}}\]
\[ \Rightarrow {\text{PC}} = 2{\text{PF}}\]
\[ \Rightarrow {\text{PF}} = \dfrac{1}{2}{\text{PC}}\]
From the above equation, it can be proved that the focal length is half of the radius of curvature of the concave mirror.
The mirror equation for the concave mirror is
\[\dfrac{1}{u} + \dfrac{1}{v} = \dfrac{1}{f}\]
Here, \[f\] is the focal length of the mirror, \[u\] is the object distance from the mirror and \[v\] is the image distance from the mirror.
When the light enters from a rarer medium to denser medium, the frequency of the light remains the same but the wavelength of the light changes.
Let the number 1 represent rarer medium and 2 represents denser medium.
The velocity \[{v_2}\] of light in the denser medium is smaller than the velocity \[{v_1}\] of light in rarer medium.
\[{v_2} < {v_1}\] …… (1)
We know the relation between the velocity and wavelength of the light.
\[v = n\lambda \]
Since the frequency remains the same, the velocity of light is directly proportional to the wavelength of light.
\[v \propto \lambda \]
Rewrite equation (1) in terms of wavelength of light.
\[{\lambda _2} < {\lambda _1}\]

Therefore, the wavelength of the light in denser medium is smaller than in rarer medium.
Hence, when the light enters a denser medium from a rarer medium, the frequency of light remains the same but the wavelength decreases.

Note:
One should be careful while proving the given statement using the ray diagram because if the angles which are the same are taken incorrectly, the final expected answer will not be derived. Also one should use the proper equation for velocity to determine the effect on wavelength when the light changes the medium.