
Draw an equilateral triangle of side 5 cm. Draw its inscribed circle. Measure the radius of the inscribed circle.
Answer
524.7k+ views
1 likes
Hint: Take the triangle as ABC. Draw base BC as 5 cm and construct the equilateral triangle with side 5 cm. Take angle bisectors of B and C. Find the center of the circle, and with the center O, draw a circle inscribed in triangle ABC.
Complete step-by-step answer:
Let us name the equilateral triangle as ABC.
First draw the line segment of 5 cm. Let us take BC = 5 cm. Then with center as B and C, draw two arcs of 5 cm length. These arcs intersect at point A.
Thus we got an equilateral triangle ABC by joining the points AB and AC.
As it’s an equilateral triangle, we know all the sides are equal which is 5 cm. Similarly all the angles of triangle ABC is similar, i.e. the angle is
Let us draw angle bisectors from B and C of the triangle and they meet at point O, i.e. angle bisectors of
Now with center O and radius as OL, draw a circle which touches the sides of
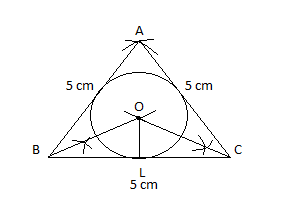
Thus we got the required figure, where an equilateral triangle of side 5 cm is drawn and a circle is inscribed in it.
Thus if we measure the radius of the inscribed circle, OL = 1.4 cm.
Hence radius, OL = 1.4 cm.
Note: We can also take angle bisectors and A and C or even B and C. We will get the same center as given in the figure. Draw OL perpendicular to BC in order to get the radius, then the construction of circle becomes easier and the circle should touch the sides of the
Complete step-by-step answer:
Let us name the equilateral triangle as ABC.
First draw the line segment of 5 cm. Let us take BC = 5 cm. Then with center as B and C, draw two arcs of 5 cm length. These arcs intersect at point A.
Thus we got an equilateral triangle ABC by joining the points AB and AC.
As it’s an equilateral triangle, we know all the sides are equal which is 5 cm. Similarly all the angles of triangle ABC is similar, i.e. the angle is
Let us draw angle bisectors from B and C of the triangle and they meet at point O, i.e. angle bisectors of
Now with center O and radius as OL, draw a circle which touches the sides of

Thus we got the required figure, where an equilateral triangle of side 5 cm is drawn and a circle is inscribed in it.
Thus if we measure the radius of the inscribed circle, OL = 1.4 cm.
Hence radius, OL = 1.4 cm.
Note: We can also take angle bisectors and A and C or even B and C. We will get the same center as given in the figure. Draw OL perpendicular to BC in order to get the radius, then the construction of circle becomes easier and the circle should touch the sides of the
Latest Vedantu courses for you
Grade 10 | CBSE | SCHOOL | English
Vedantu 10 CBSE Pro Course - (2025-26)
School Full course for CBSE students
₹35,000 per year
Recently Updated Pages
Express the following as a fraction and simplify a class 7 maths CBSE

The length and width of a rectangle are in ratio of class 7 maths CBSE

The ratio of the income to the expenditure of a family class 7 maths CBSE

How do you write 025 million in scientific notatio class 7 maths CBSE

How do you convert 295 meters per second to kilometers class 7 maths CBSE

Write the following in Roman numerals 25819 class 7 maths CBSE

Trending doubts
A boat goes 24 km upstream and 28 km downstream in class 10 maths CBSE

The British separated Burma Myanmar from India in 1935 class 10 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

What are the public facilities provided by the government? Also explain each facility

Difference between mass and weight class 10 physics CBSE

SI unit of electrical energy is A Joule B Kilowatt class 10 physics CBSE




