Question

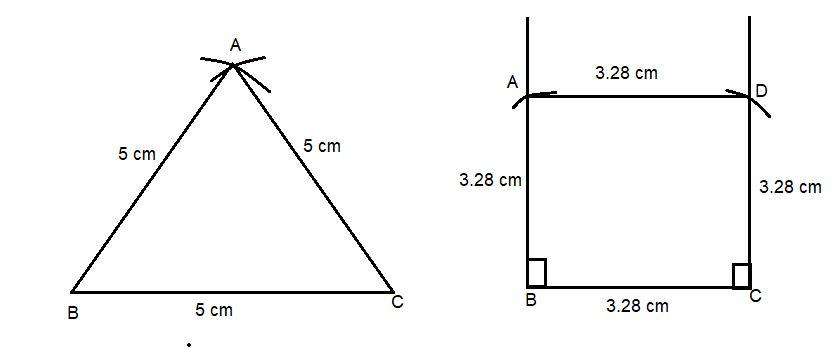
Draw an equilateral triangle of sides 5 cm. Construct a square having the same area as that of this triangle.

Answer 1

Hint: - Here we go through by first constructing the equilateral triangle and then after construction we find its area. Then we equate this area with the area of the square. From this we find the side of the square. From the help of this side we construct our required square.

Complete step-by-step solution -
Steps of construction of a triangle:
1. Draw a line segment BC of length 5cm.
2. Measure distance of 5 cm in compass. Taking B as center draws an arc.
3. Taking C as center with the same distance i.e. 5 cm draws another arc in such a way that intersects the first arc we drew.
4. Both the arcs intersect each other; name that point of intersection as A.
5. Now join the point AB and AC to formed the triangle
6. Required triangle ABC is drawn as an equilateral triangle because all the sides are equal.

Area of ABC can be calculated using the formula of equilateral triangle i.e. $A = \dfrac{{\sqrt 3 {a^2}}}{4}$
Area of $\vartriangle ABC = \dfrac{{\sqrt 3 {a^2}}}{4}$ (Here a is the side of equilateral triangle i.e. 5 cm)
By putting the value of ‘a’ we get,
Area of $\vartriangle ABC = \dfrac{{\sqrt 3 {a^2}}}{4} = \dfrac{{\sqrt 3 \times 5 \times 5}}{4} = 10.82c{m^2}$
Now we have to construct a square whose area is the same as a triangle. To solve this we have to equate the area of the square with the area of the triangle.
As we know the area of the square is${(side)^2}$. So after equating we get,
$
  {(side)^2} = 10.82c{m^2} \\
   \Rightarrow side = \sqrt {10.82c{m^2}} \\
 $
$\therefore $Side =3.28 cm.
By the help of this side we construct our square.
Steps of Construction for square:
1. Draw segment BC of length 3.28 cm.
2. Draw a line perpendicular on BC through B by the help of a protector.
Measure a distance of 3.28 cm in compass and cut this line at point A taking B as centre.
3. Draw a line perpendicular to BC through C by the help of a protector..
Measure a distance of 3.28 cm in compass and cut this line at point D taking C as a centre.
4. Join AB, CD and AD.
5. Required square ABCD is drawn.

Note: - Whenever we face such a type of question the key concept for solving the question is first construct our first diagram and then find out its area then for the second diagram whose area is the same as the first diagram. Equate the formula of the area of the second diagram to the area of the first diagram to find the value of sides. And by the help of this side we can easily draw our required diagram.