Question

Draw graph of $x-2y=4,\text{ }2x-4y=12$ on the same coordinate plane. Observe it, think of the relation between coefficient of x, coefficient of y and the constant teams and draw the inference.

Answer 1

Hint: To solve this type of question we can use the following points. If $ax+by+c=0$ and $px+qy+r=0$are the two given equations of lines then,
1. Lines are intersecting is $\dfrac{a}{p}\ne \dfrac{b}{q}$
2. Lines are parallel and intersecting if $\dfrac{a}{p}=\dfrac{b}{q}=\dfrac{c}{r}$
3. Lines are parallel and non – consisting if $\dfrac{a}{p}=\dfrac{b}{q}\ne \dfrac{c}{r}$

Complete step-by-step answer:
The two linear equation in two variables are:
1. $x-2y=4$
2. $2x-4y=12$

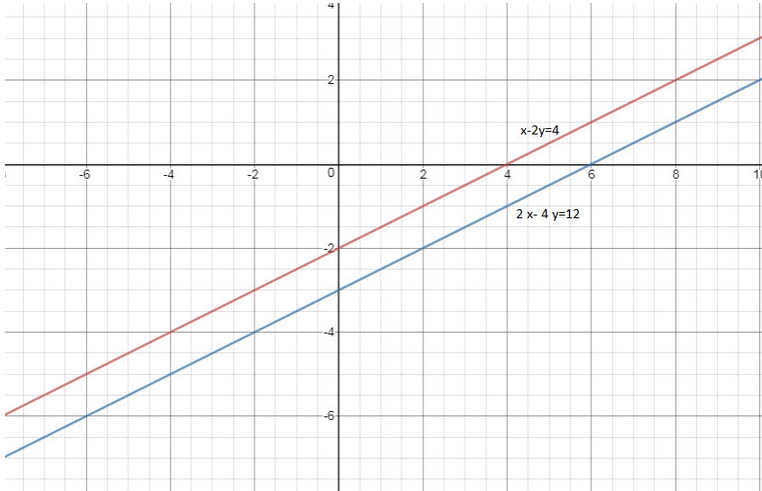
So, if the two lines are parallel their slopes should be equal.
And if they are coincident a intersecting
$\dfrac{a}{b}\ne \dfrac{p}{q}$
Comparing the given equations with
$ax+by+c=0$ and$px+qy+r=0$
We get,
$a=1\text{ }p=2$
$b=-2\text{ q}=-4$
$c=-4\text{ }r=-12$
.Here $\dfrac{1}{2}=\dfrac{-2}{-4}\ne \dfrac{-4}{-12}$
Hence these lines are parallel and not coincident. Also, parallel lines have equal slopes.
Line 1 = $x-2y=4$ transposing x we get,
$-2y=4-x$ dividing whole equation
$y=\dfrac{x}{2}-2$ by $-2$ we get,
Comparing with standard equation of time we get
$y=mx+c\text{ }m=\text{slope = }\dfrac{1}{2}$
Line 2 = $2x-4y=12$ transposing $2x$ we get,
$-4y=12-2x$ dividing whole equation by -4 we get
$y=\dfrac{1}{2}x-3$.
Comparing with standard question of line $y=mx+c$
We get,
$m=\dfrac{1}{2}$.
As the slopes of both lines are equal these given lines are parallel.

Note: If we have parallel lines which are also coincident. In that case, the lines are multiples of each other,
$ax+by+c=m\left( px+qy+r \right)$ where $m\varepsilon R$
For eg. $2x+4y+6=2\left( x+2y+3 \right)$
Нence, $2x+4y+6$ and $x+2y+3$.are parallel and coincident lines.