Question

Draw the circuit diagram of a meter bridge to show how it is based on a Wheatstone bridge.

Answer 1

Hint: Meter bridge is a simple form of potentiometer that is used in science laboratories. It is used for the determination of the unknown resistance of a conductor. It works on the principle of Wheatstone bridge. Wheatstone bridge is an electric circuit which is used to measure the unknown electrical resistance. It is used to measure low resistance precisely.

Complete step-by-step solution:

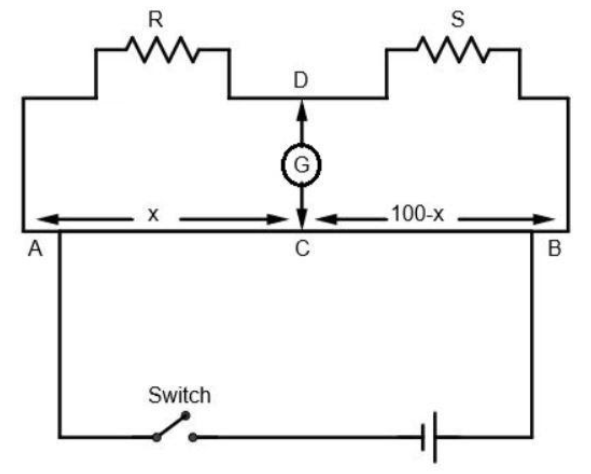
The above figure shows a meter bridge. A Meter bridge is an electrical instrument based on the Wheatstone bridge which is useful for determining the unknown resistance of any material. In this instrument, a one-meter wire is used with unknown resistance. The cross-sectional area of the wire is uniform. This wire is connected to a galvanometer. Now, as it is based on the principle of the Wheatstone bridge, we need to find the unknown resistance of the wire.

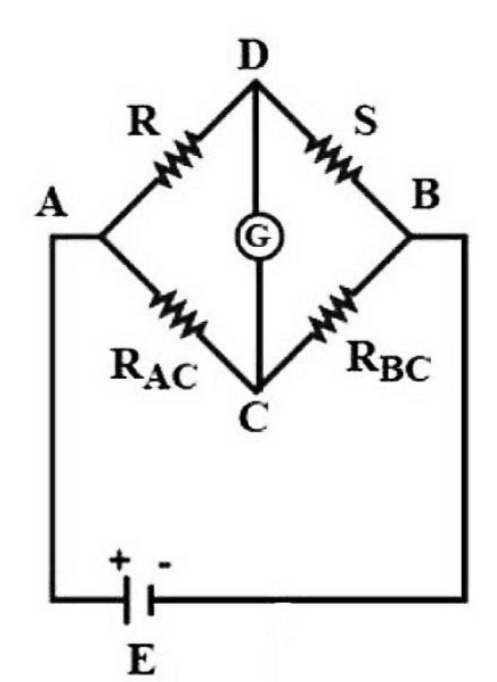
The above-given figure shows the arrangement of an equivalent Wheatstone bridge.
Let L be the length of the wire
According to principle of Wheatstone bridge,
$\dfrac { { R }_{ AD } }{ { R }_{ AC } } =\dfrac { { R }_{ BD } }{ { R }_{ BC } }$
$\Rightarrow \dfrac { { R } }{ { R }_{ AC } } =\dfrac { S }{ { R }_{ BC } }$ …………...…(1)
Now, we know, the relation between resistance and resistivity is given by,
$R=\rho \dfrac { L }{ A }$
Where R is the known resistance
             S is the unknown resistance
$\Rightarrow { R }_{ AC }=\rho \dfrac { { L }_{ AC } }{ A } ={ R }_{ 0 }\times \dfrac { x }{ L } =\dfrac { { R }_{ 0 }x }{ L }$ ……………….…(2)
Similarly,
$ { R }_{ BC }=\rho \dfrac { { L }_{ BC } }{ A } ={ R }_{ 0 }\times \dfrac { (100-x) }{ L } =\dfrac { { R }_{ 0 }(100-x) }{ L }$ …………………….(3)
Now, substituting the equation (2) and (3) in equation (1) we get,
$\Rightarrow \dfrac { R }{ \dfrac { { R }_{ 0 }x }{ L } } =\dfrac { S }{ \dfrac { { R }_{ 0 }(100-x) }{ L } }$
$\Rightarrow \dfrac { R }{ x } =\dfrac { S }{ (100-x) }$
$\Rightarrow S=\dfrac { R(100-x) }{ x }$
This is the required equation to find the value of unknown resistance from the known resistance.

Note: Under normal conditions, the bridge is said to be unbalanced where the current flows through the galvanometer. When the bridge gets balanced, no current flows through the galvanometer. The bridge is balanced by balancing the known and variable resistance. Wheatstone bridge is used to measure stress, strain, temperature, etc.