Question

Draw the graph of $x=5$ .

Answer 1

Hint: In this question, you need to understand that the given equation is of the form x=k, i.e., it represents a straight line parallel to y-axis when represented on a Cartesian plane. Also, looking at the equation, we can easily say that it passes through the point (5,0). So, you need to draw a line parallel to the y-axis and pass through the point (5,0) to represent the point on the graph.

Complete step-by-step answer:
Let us first find the general equations of the lines parallel to the y-axis.
We know the slope of the line parallel to the y-axis = slope of y-axis = $\infty =\dfrac{1}{0}$ .
Using general form of line, we get
$y=mx+c$
So, the equation of line becomes;
$y=\dfrac{1}{0}.x+c$
$\Rightarrow y-c=\dfrac{1}{0}.x$
On cross-multiplication, we get:
$0.(y-c)=x$
When c is finite;
The equation of the line parallel to y-axis come out to be;
$x=0$
When c is infinite:
We know, infinity multiplied by zero can give any value so let the value be ${{c}_{1}}$ .
We get, $x={{c}_{1}}$ .
As 0 is also a constant, the equation of line parallel to y-axis comes out to be: $x=k$
Where k is constant.
So, looking at the above equation, we can easily say that x=5 is the equation of the line i.e. parallel to y-axis. Also, looking at the equation we can easily say that the line will pass through the point (5,0). So, we will represent this line on the Cartesian plane, i.e., the graph.

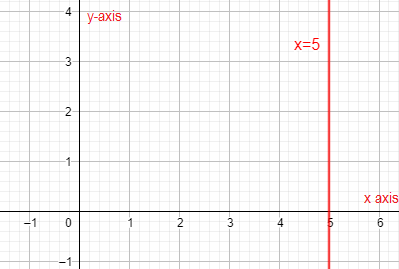
Note: Avoid using intercept form of line for the lines parallel to x-axis and y-axis as you may get one of the intercepts to be infinity. Also, remember that the term graph generally refers to the Cartesian plane. However, if you are asked about the representation on the number line, then x=5 will be a point and on the 3-D plane x=5 will represent a plane.