Question

Draw the net of a tetrahedron.

Answer 1

Hint: In order to solve this problem, we need to understand the definition of the net and how the tetrahedron looks. The geometry is the 2-dimensional shape that can be folded into a 3-dimensional solid. The tetrahedron is the shape made up of four equilateral triangles connected with common edges. The tetrahedron is also called the triangular pyramid.

Complete step-by-step answer:
To draw the net, we need to understand the meaning of a net. A geometry net is a 2-dimensional shape that can be folded to form a 3-dimensional shape or solid.
A tetrahedron is a solid composed of four triangular faces and six straight edges and four vertices.
Therefore, to construct the tetrahedron net we need to draw four equilateral triangles.
We will begin by drawing an equilateral triangle.
Let's start by drawing the line segment of BC of any measure.
It is shown as below,

Take the same distance BC in the compass and draw an arc with point B as the vertex.
Repeat the same procedure with a compass on point C.
We need to make sure that both the arcs intersect with each other.
Name the point of intersection as point A.
It is shown as below,

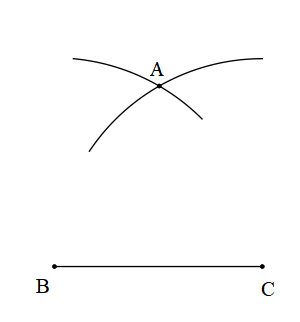
Connect the segments AB and AC and then we will get an equilateral triangle ABC.
It is shown as below,

As we know there are 4 triangular faces to a tetrahedron, We need to repeat this process for 4 times.
Taking AC as a base need to draw a similar equilateral triangle.
It is shown as below,

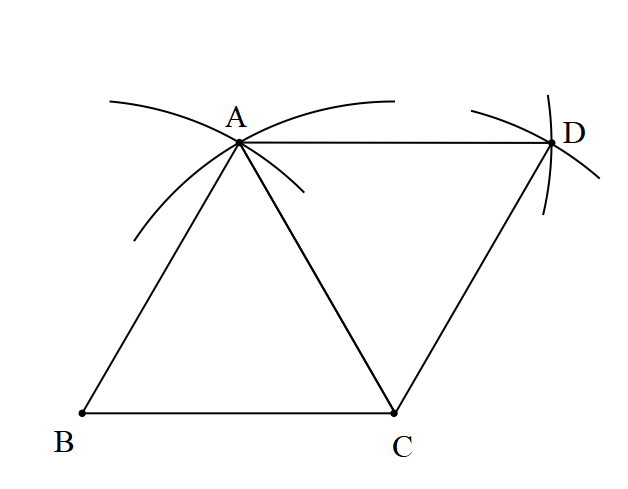
Now repeat the process third time with DC as the base.
It is shown as below,

Now, for the last equilateral triangle, we will take the base as AD.
By repeating the process we get as follows,

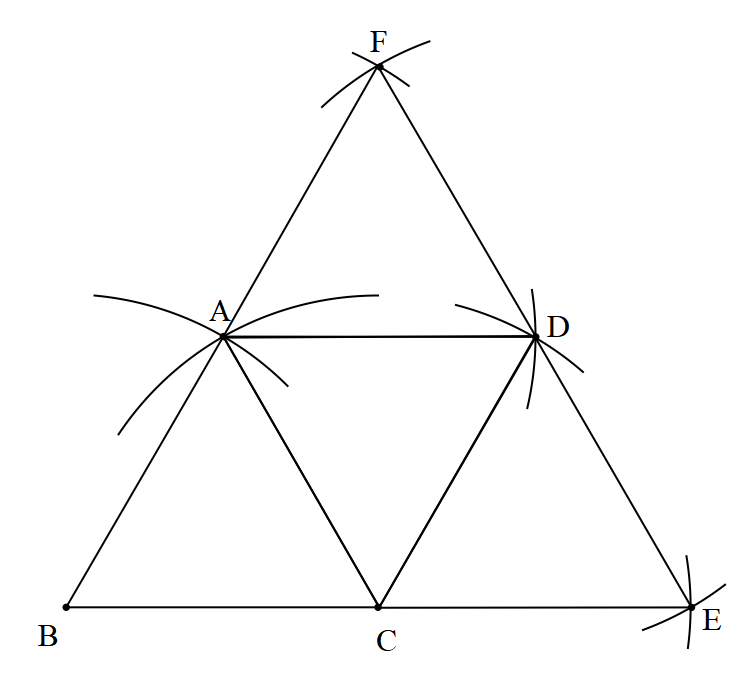
Therefore, we have completed the procedure for drawing the net for the tetrahedron.
To stick all the parts together we need to add extra cutout of paper.
It can be shown as follows,

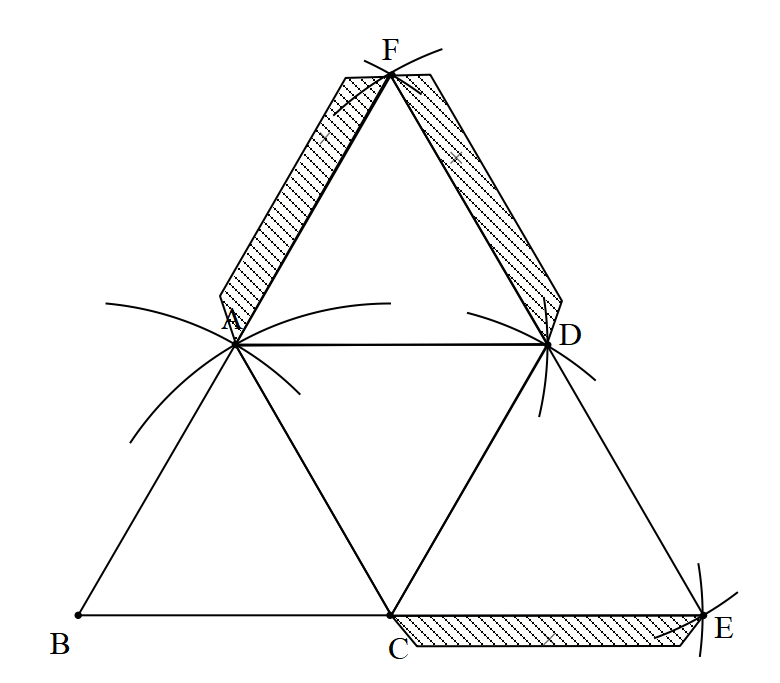
Therefore, the shaded portion is the portion that will hold the 3-dimensional solid together.
Hence, this is the required solution.

Note: We need to take care that the distance in the compass never changes and is always equal to the side of the required equilateral triangle. Also, it is important to name every vertex of the triangle.
We can check that every triangle is an equilateral triangle by measuring the angles. Every angle in the equilateral triangle is ${60}^{\circ }$ .