Question

Draw the structure of $Xe{{F}_{4}}$.

Answer 1

Hint: The structure of $Xe{{F}_{4}}$ is governed by the VSEPR theory of electron repulsion. With this idea in mind, try to predict the structure of the given compound.

Step-by-Step Solution:
Before we move onto the structure of $Xe{{F}_{4}}$ , let us first look into the VSEPR theory of electron repulsion.
VSEPR (Valence Shell Electron Repulsion) theory proposes that the geometric arrangement of terminal atoms, or groups of atoms about a central atom in a covalent compound, or charged ion, is determined solely by the repulsions between electron pairs present in the valence shell of the central atom.
The number of electron pairs around the central atom can be determined by writing the Lewis structure for the molecule. The geometry of the molecule depends on the number of bonding groups (pairs of electrons) and the number of nonbonding electrons on the central atom.
Now, with the specifics of the VSEPR theory done and accounted for, let us now move on to the specific structure of $Xe{{F}_{4}}$.
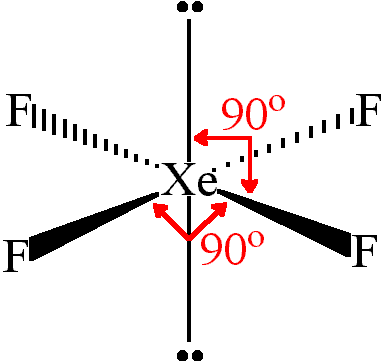
VSEPR theory predicts that $Xe{{F}_{4}}$ is square planar. There are six electron pairs around the central atom (Xe), four of which are bonding, and two are lone pairs. Thus, we have octahedral electron pair geometry, and square planar molecular geometry.

It’s possible that someone might tell you that xenon exhibits \[sp{}^\text{3}d{}^\text{2}\] hybridization. Don’t believe that. It’s been pretty well established that for the representative elements there is no d-orbital participation in the bonding in hypervalent molecules.

Note: While a traditional compound unlike $Xe{{F}_{4}}$ such as xenon hexafluoride ($Xe{{F}_{6}}$) without the presence of lone pairs in its structure would exhibit octahedral geometry with different bond angles, the presence of lone pairs increases electron repulsions leading to a square planar structure with 900 bond angles.