Question

During the festival of Holi, Ram throws a small water balloon from the ground so as to hit Shyam. Shyam is standing on top of a building of height $10m$. If the building is at a distance $20m$ away from Ram and he throws the balloon at angle ${{45}^{\circ }}$with horizontal, then the speed of projection required will be? (Given $g=10m{{s}^{-2}}$)
A. $10m{{s}^{-1}}$
B. $20m{{s}^{-1}}$
C. $30m{{s}^{-1}}$
D. $40m{{s}^{-1}}$

Answer 1

Hint:The balloon thrown by Ram follows a semi-parabolic path to reach Shyam at a height of $10m$from the ground. The balloon will acquire two components of its initial velocity, one in the x-direction and the other in the y-direction. Thus, we shall solve this problem by using the equations of a projectile.

Complete step-by-step solution:
The situation described in the given question is illustrated in the diagram given below:

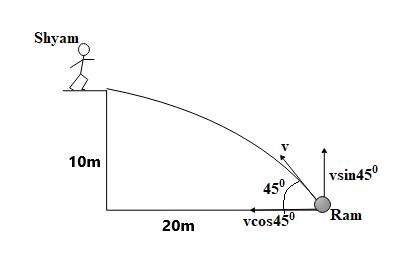
Let $v$ be the initial velocity of projection of the water- filled balloon thrown by Ram. Since the balloon is thrown at an angle of ${{45}^{\circ }}$ with the horizontal, therefore it will have the following components of its velocity:
In the x-direction: ${{v}_{x}}=-v\cos {{45}^{\circ }}$ (negative sign implies that velocity is in the negative x-direction along the horizontal.)
In the y-direction: ${{v}_{y}}=v\sin {{45}^{\circ }}$
We know that $\sin {{45}^{\circ }}=\dfrac{1}{\sqrt{2}}$ as well as $\cos {{45}^{\circ }}=\dfrac{1}{\sqrt{2}}$ .
Hence, ${{v}_{x}}=-\dfrac{v}{\sqrt{2}}$ and ${{v}_{y}}=\dfrac{v}{\sqrt{2}}$ . …………….. equation (1)
The maximum height of a projectile motion is given by:
$H=\dfrac{{{\left( {{v}_{y}} \right)}^{2}}}{2g}$
Where,
$H=$ maximum height of the projectile motion
${{v}_{y}}=$ velocity of the projectile along the vertical (in y-direction)
$g=$ acceleration due to gravity
The only unknown quantity is the initial velocity of projection, $v$ of the balloon.
Here, we are given that
$y=H=10m,\text{ }x=20m,\text{ }{{v}_{x}}=-\dfrac{v}{\sqrt{2}},\text{ }\theta ={{45}^{\circ }},\text{ }g=10m{{s}^{-2}}$
 From equation (1):
$\Rightarrow H=\dfrac{{{\left( \dfrac{v}{\sqrt{2}} \right)}^{2}}}{2g}$
$\begin{align}
  & \Rightarrow H=\dfrac{{{v}^{2}}}{\left( 2 \right)2g} \\
 & \Rightarrow 10=\dfrac{{{v}^{2}}}{4\left( 10 \right)} \\
 & \Rightarrow {{v}^{2}}=\left( 400 \right) \\
\end{align}$
$\begin{align}
  & \Rightarrow v=\sqrt{400} \\
 & \Rightarrow v=\pm 20 \\
\end{align}$
Ignoring the negative value, we get that the initial velocity of projection of the balloon is $20m{{s}^{-1}}$.

Therefore, the correct option is (B) $20m{{s}^{-1}}$.

Note:
Another way of solving the problem was by substituting all the given values in the equation of range of the projectile. Range of a projectile is the horizontal distance travelled by the body during its projectile motion. As the balloon hits Shyam, it is stopped in the middle of its projectile motion. If the balloon would have missed Shyam, it would have travelled another $20m$ to the left to complete its path.