Question

Each exterior angle of a regular hexagon is of
(a) 120
(b) 80
(c) 100
(d) 60

Answer 1

Hint: Here, at first we will find the measure of interior angle of a regular hexagon and then we will subtract the obtained value from 180 degrees to get the value of exterior angles.

Complete step-by-step answer:

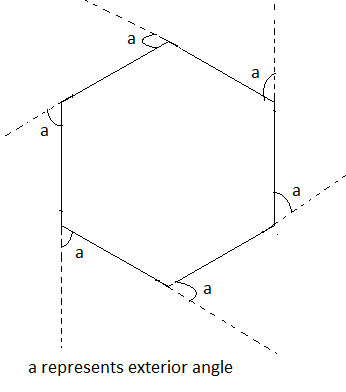
Since, we know that in a regular polygon all the sides of the polygon are equal.
Similarly, a regular hexagon is a polygon with six equal sides and angles. The triangle formed by joining the centre with all the vertices are equal in size and are equilateral triangles and all the interior angles of a regular hexagon are also equal.
Therefore, all the exterior angles are also equal.
Now, we know that the sum of all the exterior angles of a polygon is equal to 360 degrees.
The formula used for finding the measure of interior angle of a polygon is given as:
$d=\dfrac{180\left( n-1 \right)}{n}$, “d” represents interior angle and n is the number of sides in the polygon.
Since, for the hexagon we have n = 6. So, on putting n = 6 in above equation, we get:
\[\begin{align}
  & d=\dfrac{180\left( 6-2 \right)}{6} \\
 & d=\dfrac{180\times 4}{6} \\
 & d=120 \\
\end{align}\]
So, the value of d or interior angle is 120 degrees.
Therefore, the exterior angle of a regular hexagon will be = 180 – 120 = 60 degrees.
Hence, option (d) 60 is the correct answer.

Note: Students should know the properties of a regular hexagon that all the exterior angles are equal as well as all the interior angles are also equal.