Question

Eight drops of equal size are falling through air with steady velocity of 10cm/s. If the drops coalesce, what would be its terminal velocity?

Answer 1

Hint: Any change with the value of terminal velocity of the new drop will be due to the change in the radius of the drop as the other parameters, like viscosity, density of drop fluid and air can be considered invariable.

Complete answer:

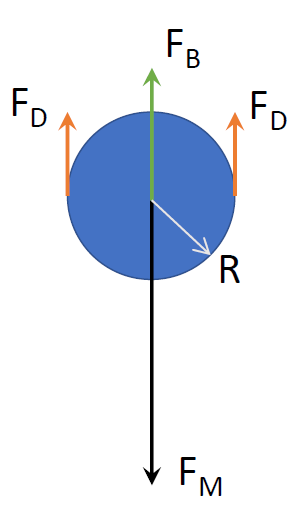
Consider the diagram where the blue disc represents a drop of radius . At terminal velocity all the forces acting on the droplet are balanced. Let $\rho ,\sigma $ denote the densities of the fluid of the drop and the medium. Generally, $\sigma $will be equal to density of air, which will be smaller than the density of the drop. Weight of the fluid, ${F_M} = \rho g\left( {\dfrac{{4\pi {R^3}}}{3}} \right)$. Here, $g$ acceleration due to gravity, and the terms in the bracket is the volume of the drop. Buoyancy forces acting on the drop, ${F_B} = \sigma g\left( {\dfrac{{4\pi {R^3}}}{3}} \right)$. Suppose the terminal velocity be given by ${u_T}$. At this velocity, the drag forces acting on the drop ${F_D} = 6\pi R\eta {u_T}$.
At terminal velocity, ${F_M} = {F_D} + {F_B}$.
Substituting each expression in above equation, we get,
$ \Rightarrow \rho g\left( {\dfrac{{4\pi {R^3}}}{3}} \right) = \sigma g\left( {\dfrac{{4\pi {R^3}}}{3}} \right) + 6\pi R\eta {u_T}$
After solving it for ${u_T}$, we get following expression:
$ \Rightarrow {u_T} = \dfrac{{2g{R^2}(\rho - \sigma )}}{{9\eta }}$
Thus, the terminal velocity of the drop is proportional to square of its radius. Let ${R_1}$be the new radius of the drop after combining eight drops. Therefore, new volume of the drop is as follows:
$ \Rightarrow \dfrac{{4\pi R_1^3}}{3} = 8 \times \dfrac{{4\pi {R^3}}}{3}$
After simplifying for ${R_1}$, we get,
$\begin{gathered}
   \Rightarrow R_1^3 = 8{R^3} \\
   \Rightarrow {R_1} = 2R \\
\end{gathered} $
Thus the new drop has twice as much the radius of the smaller drop. Since the terminal velocity is proportional to square of the radius of drop, and if we consider the new terminal velocity as ${u_{T1}}$, then we can relate the old and new terminal velocities with the corresponding radii as follows:
$ \Rightarrow \dfrac{{{u_{T1}}}}{{{u_T}}} = \dfrac{{R_1^2}}{{{R^2}}}$. This relation was used since the other parameters like, density, viscosity remain constant for both drop sizes. Substituting the relation between the radii and ${u_T}$=10cm/s, we get
${u_{T1}} = 10 \times \dfrac{{{{(2R)}^2}}}{{{R^2}}} = 10 \times 4 = 40$.
Thus the new terminal velocity is equal to 40cm/s.

Note: When there are many forces acting on a body it is better to determine each force individually, simplify if possible and then substitute them in the balance equation.