Question

Equation of a stationary wave is given by
A. $y = A\sin (kx - \omega t)$
B. $y = 2A\sin kx.\cos \omega t$
C. $y = A\cos 2\pi (kx - \dfrac{t}{T})$
D. $y = A\cos (2\pi t/I)$

Answer 1

Hint: The wave can be defined as a disturbance which propagates or travel energy from one place to another without the transport of matter. Characteristics of waves is given by crest and trough, amplitude, wavelength, frequency and phase.

Complete answer:
We have studied that stationary waves are produced by superposition of two progressive waves of equal amplitude and frequency, travelling with the same speed in opposite directions. The stationary waveform does not move through medium; energy is not away from the source. The amplitude of a stationary wave can vary from zero at a node to maximum at an antinode, and depends on position along the wave. In this wave, between nodes all particles are at the same phase.

Diagram of stationary Wave is given below;

               

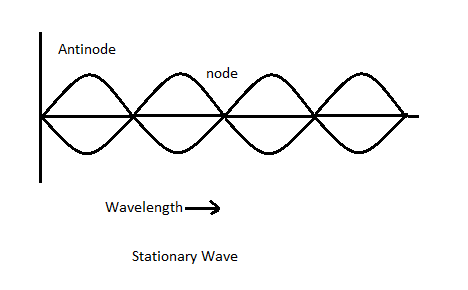
We know that stationary waves are a combination of two waves moving in opposite directions having the same frequency and amplitude. So let's consider a wave of amplitude $A$ travelling in positive X- direction and another wave of amplitude $A$ travelling in negative direction. Their displacement equation can be given as;
${y_1} = A\sin (\omega t - kx)$ and ${y_2} = A\sin (\omega t + kx)$
Now we can apply superposition principle here, so the displacement of the resultant wave is given by; $y = {y_1} + {y_2}$
$
  y = A\sin (\omega t - kx) + A\sin (\omega t + kx) \\
  \Rightarrow y = 2A\sin \dfrac{{(\omega t + kx + \omega t - kx)}}{2}\cos \dfrac{{(\omega t + kx + \omega t - kx)}}{2} \\
  \Rightarrow y = 2A\sin \omega t.\cos kx \\
$

So, the correct answer is “Option B”.

Note:
So with the help of the equation of stationary waves we can observe some important features of stationary waves. Some musical instruments for example sitar, violin and guitar etc. produce stationary waves.