Question

Equation of plane progressive wave is given by $y = 0.6\sin 2\pi \left( {t - \dfrac{x}{2}} \right).$ On reflection from a denser medium its amplitude becomes $2/3$ of the amplitude of the incident wave. The equation of the reflected wave is
A. $y = 0.6\sin 2\pi \left( {t + \dfrac{x}{2}} \right)$
B. $y = - 0.4\sin 2\pi \left( {t + \dfrac{x}{2}} \right)$
C. $y = 0.4\sin 2\pi \left( {t + \dfrac{x}{2}} \right)$
D. $y = - 0.4\sin 2\pi \left( {t + \dfrac{x}{2}} \right)$

Answer 1

Hint: When a wave is reflected back after incidence onto the rigid support or denser medium that, first the path is reversed and second the phase difference between the incident and reflected wave is of $\pi $.

Complete step by step solution:

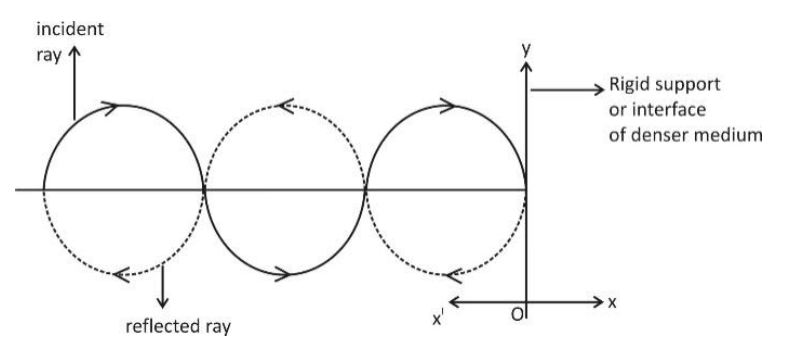
The incident wave is given$y = 0.6\sin 2\pi \left( {t - \dfrac{x}{2}} \right)$comparing it by$y = A\sin 2\pi \left( {t - \dfrac{x}{2}} \right)$$A = 0.6$ So, the amplitude of reflected wave,
${A^1} = \dfrac{2}{3} \times A $(given)
Or, ${A^|} = \dfrac{2}{3} \times 0.6$
Or, $\boxed{{A^|} = 0.4}$
$ \bullet $ For writing the equation of the wave –
(i) The direction of reflected wave beams opposite to that of the incident so on the plane$\left( { - x} \right)$in the place of$\left( { + x} \right)$.
(ii) Here the wave is reflected from the duggar medium so there will be a phase difference of $\pi $ between incident and reflected wave.
$ \to $The equation of incident wave is given,
$ye^\circ = 0.6\sin \left( {2\pi t} \right) - \dfrac{{2\pi x}}{2}$

So, the equation of reflected wave will be,
${y_R} = {A^|}\sin \left[ {2\pi t - \dfrac{{2\pi \left( { - x} \right)}}{2} + \pi } \right]$
${y_R} = 0.4\sin \left[ {2\pi t + \dfrac{{2\pi x}}{2} + \pi } \right]$
$y_R = - 0.4\sin \left( {2\pi t + \dfrac{{2\pi x}}{2}} \right)$
${y_R} = - 0.4\sin 2\pi \left( {t + \dfrac{x}{2}} \right)$

Hence option (D) is correct.

Additional information: During propagation of a plane progressive mechanical wave amplitude of all the particles is equal, the particle of the medium execute SHM(simple harmonic motion) and wave velocity depends upon the nature of the medium and all the particles are vibration in different phase.

Note: The progressive waves distribute energy from a point source to a surrounding area. They move like such energy in the form of vibrating particles or fields. The particle movement is a series of compressions and rarefactions. The examples are sound waves and some earthquake waves.