Question

Establish a relation between electric current and drift velocity. OR prove that the current density of metallic conductors is directly proportional to the drift speed of electrons.

Answer 1

Hint Here, we know that the concept of electric current and drift velocity so that we can analyze the electron w velocity should understand that current density J is a vector quantity defined as the current flowing per unit area measured in a normal direction to the charge flow direction.
Useful formula:
Current density,
\[J = pv\]
Where,
$J$ is electric current density,
$p$ charge the velocity,
$v$ velocity of density,

Complete step by step procedure
Relation between electric current and drift velocity.
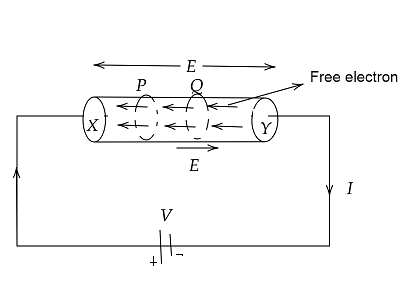
Consider a uniform metallic wire $XY$ of length $1$ and cross-sectional area $A$. A potential difference V is applied across the ends $X$ and $Y$ of the wire.
At each point of the force wire, this causes an electric field.
\[E = \dfrac{V}{l}........\left( i \right)\]
This causes an electric field at each point of the force wire,${V_d}$ The opposite of the electric field's direction.
Current in wire \[I = \dfrac{q}{t}..........\left( i \right)\]
The distance traversed by each electron in time \[t = average\,velocity\]$X$ time \[ = {V_d}t\]
The total charge flowing in time $t$is equal to the total charge on the electrons present within the cylinder if we consider two planes $P$ and $Q$ at a distance ${V_d}$ in a conductor.
The volume of this cylinder is equal to cross sectional area $X$ height
$A{V_d}t$
If $n$ The number of free electrons per unit volume in the wire is then equal to the number of free electrons in the cylinder to $nA{V_d}t$

then,
 the total charge flowing through a cross section of the wire.
\[q = \left( {nA{V_d}t} \right)\left( { - e} \right) = - neA{V_d}t.........\left( {iii} \right)\]
Therefore,
Current flowing in the wire,
\[I = tq = t - v\]​
\[\;currentI = - neA{V_d}.......\left( {iv} \right)\]
This is the relation between current and drift velocity. Negative sign shows that the direction of current is opposite to the drift velocity
\[Numericaly\;I = - neA\tau d...............\left( v \right)\]
Therefore, Current density,
\[J = \dfrac{l}{A}.\]
Rearranging the equation,
We get,
\[ \Rightarrow JAI = d\]
Here,
We get,
\[ \Rightarrow J\alpha D\]
Hence,
This is the metallic conductor's current density that is directly proportional to the drift velocity.

Note According to that a drift velocity is the average velocity obtained by charged particles in a medium due to an electrical field, such as electrons. In general, at Fermi velocity, an electron in a conductor will spread spontaneously, leading to an average velocity of zero.