Question

Explain polarization of light by reflection and arrive at Brewster’s Law from it.

Answer 1

Hint:Recall the concept of polarization of an ordinary light. Use this concept and draw the diagram for polarization of light by reflection. From this diagram, determine the value of angle of refraction in terms of Brewster’s angle. Use the expression for Snell’s law and substitute the value of angle of refraction in terms of Brewster’s law in this formula and derive the relation between the Brewster’s angle and refractive index of the medium.

Complete answer:
The phenomenon in which the vibrations of an ordinary light are confined in a single plane is known as polarization of light. The diagram representing the polarization of the ordinary light is as follows:

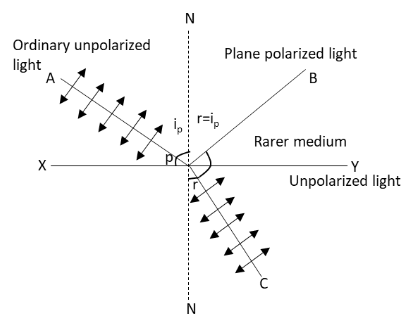
From the above equation, we can conclude that if the unpolarized light is incident on the boundary between the two media which are transparent, the light which is reflected is polarized in such a direction that its electric vector is perpendicular to the plane of incidence and the angle between the reflected ray and the refracted ray of light is a right angle.

Therefore, we can conclude that the reflected wave is polarized completely when the reflected ray is perpendicular to the refracted ray. The angle of incidence denoted in the above diagram is known as Brewster’s angle \[{i_p}\].

From the above diagram, we can write the equation
\[{i_p} + r = \dfrac{\pi }{2}\]
Here, \[r\] is the angle of reflection which is equal to the angle of refraction.
We know the expression for Snell’s law is
\[\mu = \dfrac{{\sin i}}{{\sin r}}\]

We can rewrite this equation for refractive index for this case as
\[\mu = \dfrac{{\sin {i_p}}}{{\sin r}}\]
Substitute \[\dfrac{\pi }{2} - {i_p}\] for \[r\] in the above equation.
\[\mu = \dfrac{{\sin {i_p}}}{{\sin \left( {\dfrac{\pi }{2} - {i_p}} \right)}}\]
\[ \Rightarrow \mu = \dfrac{{\sin {i_p}}}{{\cos {i_p}}}\]
\[ \therefore \mu = \tan {i_p}\]

This is the required expression for Brewster's law.

Note: The students should keep in mind that the light is polarized when its vibrations are confined in a single plane and the light is unpolarized when its vibrations are in more than one plane. Also the students may think how the value in the denominator after substitution of the angle of refraction changes to cosine value. The students should keep in mind that the sine of ninety minus an angle is equal to cosine of the angle.