Question

Explain the construction and working of a Bainbridge mass spectrometer. Mention its use.

Answer 1

Hint:For this question, we have to explain the Bainbridge mass spectrometer. We have to mention how it is made and how this device helps us to make our work easier. This can be done by making a diagram. For its application, we have to write where it can be used.

Step by step answer:Bainbridge mass spectrometer is a device which is used for measuring atomic mass of the isotopes of any element to the utmost accuracy.
 

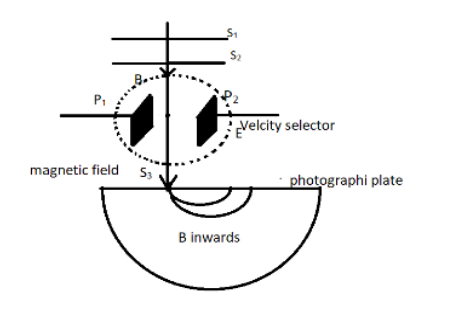
A Bainbridge mass spectrometer basically consists of a discharge tube which produces ions. The discharge tube discharges a beam of positive ions into a tube. These positive ions are produced when one or more electrons are removed from any atom. The tube has two slits named ${S_1}$ and ${S_2}$ which makes them collimated. After that the beam of positive charge passes through a velocity selector. This velocity selector allows only the particles of a given velocity. This velocity selection is done by the combined action of magnetic field and electric field. This field consists of two plates ${P_1}$ and ${P_2}$ . The magnetic field and electric field are at perpendicular to each other which nullifies their effect and hence they don’t create any deflection in the particle. Let $B$ be the magnetic field and $E$ be the electric field.
Force exerted on a particle on a particle due to the magnetic field is,
$Forc{e_m} = qBv$
Here $B$ is the magnetic field, $q$ is the charge on the particle and $v$ is the velocity of the particle.
Force exerted on a particle on a particle due to the electric field is,
$Forc{e_e} = qE$
Here $E$ is the electric field and $q$ is the charge on the particle.
As the force exerted on a particle on a particle due to the magnetic field is nullifying force exerted on a particle on a particle due to the electric field,
$ \Rightarrow qBv = qE$
$ \Rightarrow v = \dfrac{E}{B}$
So only the particles with the above velocity will pass the velocity selector.
After the velocity selector, the particles pass through another slit ${S_3}$ and enters the vacuum chamber. This chamber has a strong magnetic field of ${B'}$ which acts at right angle to the plane of paper. This directs the particles in a centripetal way and causes the particles to strike the photographic plane.
${B'}qv = \dfrac{{m{v^2}}}{R}$
Here ${B'}$ is the electric field in the vacuum, $q$ is the charge on the particle, $v$ is the velocity of the particle, $m$ is the mass of the particle, and $R$ is radius of the circular path the particle followed before striking the photographic plate.
$ \Rightarrow m = {B'}qvR$
If we know the value of all the variables, we can easily calculate the mass of the particle.

Note: It is very important to know the values of the magnetic field and the electric field to calculate the value of the mass. Also to measure the mass, we have to ionise the element whose mass we have to calculate. This can be done using the process of ionisation of atoms. It’s done just before, when the particles enter the tube.