Question

Explain the inconsistency of Ampere’s circuital law during charging of a capacitor. Define displacement current.

Answer 1

Hint: Ampere’s circuital law gives an expression that relates current in the circuit and line integral of magnetic field. At the time when ampere gave this law, that time it seemed correct according to the knowledge of humans at that time. It is only after Maxwell realized the case where Ampere’s law is invalid.

Complete answer:
After Maxwell thought of a case in which the law is not valid, there came some inconsistency in Ampere’s circuital law. Maxwell removed this inconsistency and introduced additional terms to the original Ampere’s law, called displacement current and hence since that, the law is called Maxwell Ampere’s law.
Ampere’s law (original) - $\oint{\vec{B}.\overrightarrow{dl}}={{\mu }_{{}^\circ }}i$
Maxwell Ampere’s law - $\oint{\vec{B}.\overrightarrow{dl}}={{\mu }_{{}^\circ }}i + \mu_\circ i_d$
Now, displacement current – Whenever there is a change in the electric field (and hence electric flux) in the region, it results in a special type of current in the region, called displacement current. Mathematically it is proportional to the rate of change of electric flux in the region.
i.e. $i_d = \mu_\circ\dfrac{d{\phi_E}}{dt}$
Now, coming to inconsistency:
In the original Ampere’s law: $\oint{\vec{B}.\overrightarrow{dl}}={{\mu }_{{}^\circ }}i$
‘i’ is the current enclosed by the loop. In the case of a normal complete circuit, current enclosed is the actual current flowing in the circuit and if the battery voltage is constant, there can’t be any change in electric field. Thus displacement current in that case is zero. In these types of cases, law is valid.

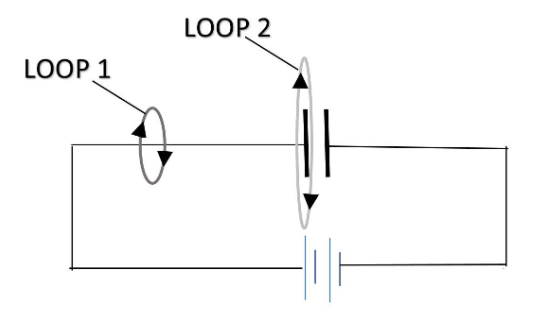
But, if we take the loop (see loop2 in the figure) enclosing half of the capacitor in a capacitive circuit, then the current enclosed in the circuit is zero as no current flows in circuit through capacitor (Note that it flows through the circuit only till capacitor charge fully, after that it stops flowing in the circuit too). Hence in that case $i =0$.
But we can take both the loops and the laws must be valid. This was the consistency.
The explanation of this was that when a battery is connected to the capacitor, the electric flux linked with it changes and hence displacement current is generated.
Hence for second loop, law becomes $\oint{\vec{B}.\overrightarrow{dl}}={{\mu }_{{}^\circ }}i_d$

Note:
Note in a circuit, where a capacitor is present, the circuit becomes open. Hence the current can’t flow through an open circuit. Therefore the current ‘i’ which is called conventional current becomes zero. To explain this phenomenon, displacement current is introduced and it is important to note that for a given circuit where both currents have their own values simultaneously, the magnitudes of both the currents are equal.