
Figure shows a semicircle that is the graph of the equation $y=\sqrt{6x-{{x}^{2}}}$. If the semicircle is rotated ${{360}^{\circ }}$ about the $x-$axis, calculate the volume of the sphere that is created. \[\]
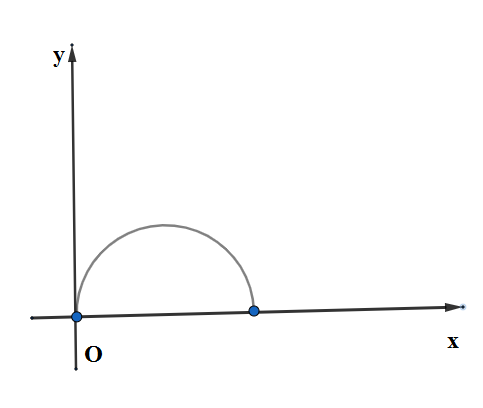
A.$6\pi $ \[\]
B. $12\pi $ \[\]
C. $18\pi $ \[\]
D. $24\pi $ \[\]
E.$36\pi $ \[\]
Answer
556.2k+ views
Hint: We denote the other point of intersection except origin as A. We find the coordinate of A by finding the solutions of $y=\sqrt{6x-{{x}^{2}}}=0$. We find OA as the diameter of the rotating sphere and find the volume of sphere $V=\dfrac{4}{3}\pi {{r}^{3}}$ where $r$ is the radius of the sphere.
Complete step-by-step solution:
We see in the figure that a semicircle is present whose one end is at the origin is defined by the equation
\[y=\sqrt{6x-{{x}^{2}}}........\left( 1 \right)\]
We denote the other end of the semicircle lying on the positive $x-$axis as A.
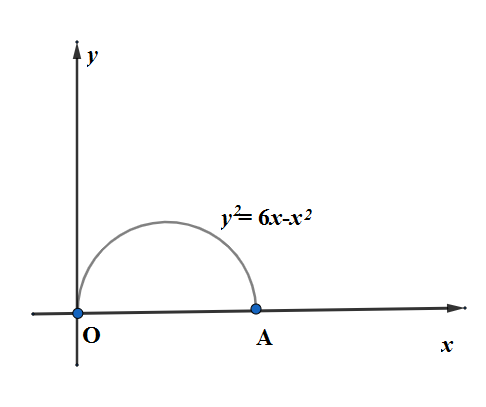
Since the equation of $x-$axis is $y=0$ . So we can find the coordinates of A since the semicircle A lies on the $x-$axis when $y=\sqrt{6x-{{x}^{2}}}=0$. So we have;
\[\sqrt{6x-{{x}^{2}}}=0\]
We square both sides of above equation to have;
\[\Rightarrow 6x-{{x}^{2}}=0\]
We factorize by taking $x$ common in the above step and have;
\[\Rightarrow x\left( 6-x \right)=0\]
Since the product of the two factors is zero one of them must be zero. So we have;
\[\begin{align}
& \Rightarrow x=0\text{ or }6-x=0 \\
& \Rightarrow x=0\text{ or }x=6 \\
\end{align}\]
So we have two roots of the equation $x=0,6$. So when $x=0,y=0$ we have the coordinate of the origin $O\left( 0,0 \right)$ and when $x=6,y=0$ we have a coordinate of $A\left( 6,0 \right)$. So the diameter of the circle is $OA=6$ units. \[\]
We are given the question that the semicircle is rotated ${{360}^{\circ }}$ about the $x-$axis and creates a sphere. So the diameter of the sphere is $OA=6$ units. So the radius $r$ of the sphere is $r=\dfrac{OA}{2}=\dfrac{6}{2}=3$ units. Then volume $V$ of the sphere in cubic units is
\[V=\dfrac{4}{3}\pi {{r}^{3}}=\dfrac{4}{3}\pi {{\left( 3 \right)}^{3}}=\dfrac{4}{3}\pi \left( 27 \right)=4\times 9\pi =36\pi \]
So the correct option is E.
Note: We note that the question presumes that the semicircle is not displaced from the original end points O and A when it's rotated about the $x-$axis. We can alternatively find the radius by squaring the given equation $y=\sqrt{6x-{{x}^{2}}}$ and then comparing it with general equation of circle ${{\left( x-a \right)}^{2}}+{{\left( y-b \right)}^{2}}={{r}^{2}}$ where $r$the radius is and $\left( a,b \right)$ is the centre of the circle. The other semi-circle fourth quadrant will have the equation$y=-\sqrt{6x-{{x}^{2}}}$.
Complete step-by-step solution:
We see in the figure that a semicircle is present whose one end is at the origin is defined by the equation
\[y=\sqrt{6x-{{x}^{2}}}........\left( 1 \right)\]
We denote the other end of the semicircle lying on the positive $x-$axis as A.
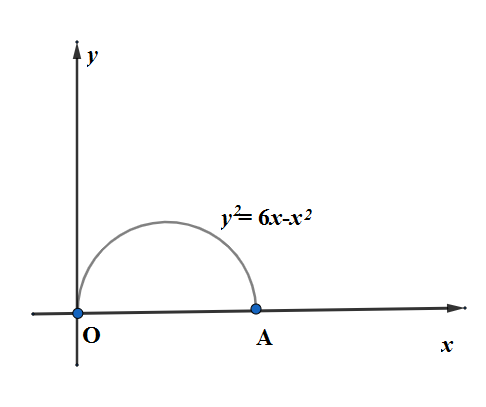
Since the equation of $x-$axis is $y=0$ . So we can find the coordinates of A since the semicircle A lies on the $x-$axis when $y=\sqrt{6x-{{x}^{2}}}=0$. So we have;
\[\sqrt{6x-{{x}^{2}}}=0\]
We square both sides of above equation to have;
\[\Rightarrow 6x-{{x}^{2}}=0\]
We factorize by taking $x$ common in the above step and have;
\[\Rightarrow x\left( 6-x \right)=0\]
Since the product of the two factors is zero one of them must be zero. So we have;
\[\begin{align}
& \Rightarrow x=0\text{ or }6-x=0 \\
& \Rightarrow x=0\text{ or }x=6 \\
\end{align}\]
So we have two roots of the equation $x=0,6$. So when $x=0,y=0$ we have the coordinate of the origin $O\left( 0,0 \right)$ and when $x=6,y=0$ we have a coordinate of $A\left( 6,0 \right)$. So the diameter of the circle is $OA=6$ units. \[\]
We are given the question that the semicircle is rotated ${{360}^{\circ }}$ about the $x-$axis and creates a sphere. So the diameter of the sphere is $OA=6$ units. So the radius $r$ of the sphere is $r=\dfrac{OA}{2}=\dfrac{6}{2}=3$ units. Then volume $V$ of the sphere in cubic units is
\[V=\dfrac{4}{3}\pi {{r}^{3}}=\dfrac{4}{3}\pi {{\left( 3 \right)}^{3}}=\dfrac{4}{3}\pi \left( 27 \right)=4\times 9\pi =36\pi \]
So the correct option is E.
Note: We note that the question presumes that the semicircle is not displaced from the original end points O and A when it's rotated about the $x-$axis. We can alternatively find the radius by squaring the given equation $y=\sqrt{6x-{{x}^{2}}}$ and then comparing it with general equation of circle ${{\left( x-a \right)}^{2}}+{{\left( y-b \right)}^{2}}={{r}^{2}}$ where $r$the radius is and $\left( a,b \right)$ is the centre of the circle. The other semi-circle fourth quadrant will have the equation$y=-\sqrt{6x-{{x}^{2}}}$.
Recently Updated Pages
Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Trending doubts
The shortest day of the year in India

Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

What is the median of the first 10 natural numbers class 10 maths CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

State and prove converse of BPT Basic Proportionality class 10 maths CBSE




