Question

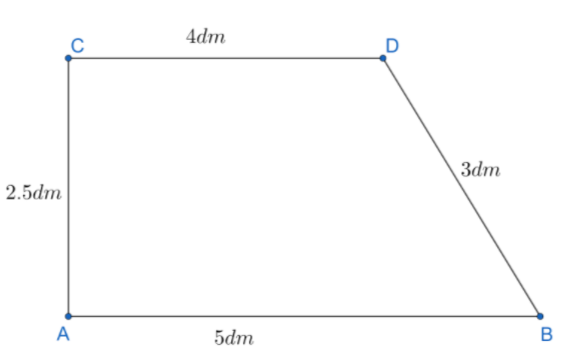
Find the area and perimeter of the trapezium given below:

Answer 1

Hint: We know that the perimeter of a figure is equal to the sum of all sides of that figure to find the perimeter of the given trapezium. To find the area of the trapezium, we draw a line parallel to side AC and we convert the given trapezium into a rectangle and triangle. We find the area of the rectangle and triangle first and then add together to get the total area of the trapezium.

Complete step-by-step solution:
Given that we have a trapezium and we need to find the perimeter and area of that trapezium.
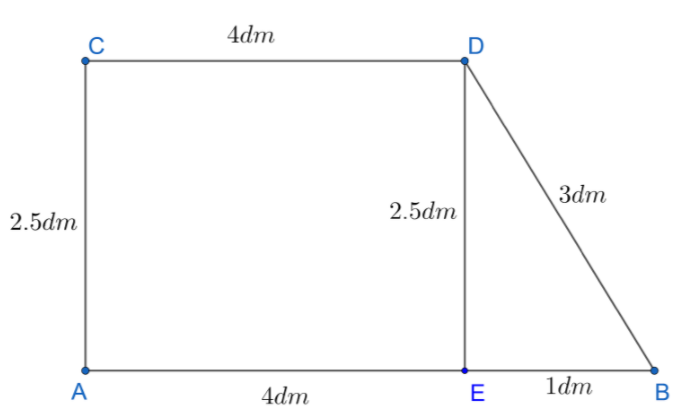
Let us start solving by drawing a line parallel to side AC from point D. We get the figure as shown below:

We know that that the perimeter of a figure is equal to the sum of the length of all of its sides.
Perimeter of trapezium ABCD = 2.5dm + 5dm + 4dm +3dm.
Perimeter of trapezium ABCD = 14.5dm ---(1).
From the figure, we can see that the area of trapezium ABCD = area of Rectangle AEDC + area of triangle DEB ---(2).
We know that area of the rectangle with length ‘l’ and breadth ‘w’ is defined as $A=l\times w$.
Area of the Rectangle AEDC = $4dm\times 2.5dm$.
Area of the Rectangle AEDC = $10d{{m}^{2}}$ ---(3).
We know that area of the triangle with base ‘b’ and height ‘h’ is $A=\dfrac{1}{2}\times b\times h$. Here base length of the triangle DEB is 1dm and height of the triangle is 2.5dm.
Area of the Triangle DEB = $\dfrac{1}{2}\times 1\times 2.5$.
Area of the Triangle DEB = $1.25d{{m}^{2}}$ ---(4).
Substitute equation (3), (4) in equation (1).
Area of trapezium ABCD = 10 + 1.25.
Area of trapezium ABCD = $11.25d{{m}^{2}}$.
$\therefore$ We have got the perimeter of the trapezium ABCD is 14.5dm and Area of trapezium is $11.25d{{m}^{2}}$.

Note: We should not add a perimeter of the rectangle and perimeter of the triangle to get the perimeter of the trapezium. As the perimeter is only the sum of all sides, we should not make up new sides for the given figure. Whenever we get a figure that doesn’t have any rectangle and triangle, we convert them into them to get the required result.