Question

Find the area of a regular octagon given the radius of circle circumscribing it as r.

Answer 1

Hint: Given an equation is an analytical and geometrical problem dealing with a regular octagon with a circle of radius r circumscribing it. We should first analyze such problems by drawing the figure of the question and then plan the sequence of actions to solve the required problem and get to the correct answer.

Complete step-by-step answer:

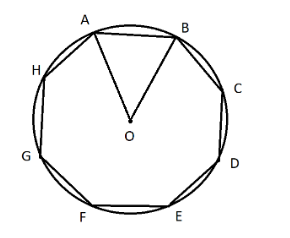
In the question, we are given a regular octagon with a circle of radius r circumscribing the octagon. We first draw the figure and then analyze the problem. So, we have to find the area of the regular octagon inscribed in a circle of radius r.
Hence, length of AO $ = $ radius of circle $ = $ r
Similarly, length of BO $ = $ radius of circle $ = $ r
Regular octagon has all sides equal.
Thus angle subtended by each edge of regular octagon at centre of the circle is equal
So, \[\angle AOB = \dfrac{{{{360}^ \circ }}}{8} = {45^ \circ }\]
Now, area of $ \Delta AOB $ = $ \dfrac{1}{2}{r^2}\sin \theta $
 $ = \dfrac{1}{2}{r^2}\sin {45^ \circ } $
 $ = \dfrac{1}{2}{r^2}\dfrac{1}{{\sqrt 2 }} $
 $ = \dfrac{{{r^2}}}{{2\sqrt 2 }} $
Now, to find the area of a regular octagon, we have to find areas of all the eight triangles separately and add them all.
Since all the triangles thus formed are congruent to each other with measure of all the sides being equal. So, the area of all the triangles would be equal.
Area of Octagon $ = $ Area of $ 8 $ triangles $ = $ $ 8 \times $ ( area of $ \Delta AOB $ )
Thus, area of octagon $ = \dfrac{{8{r^2}}}{{2\sqrt 2 }} $
 $ = \dfrac{{4{r^2}}}{{\sqrt 2 }} $
 $ = 2\sqrt 2 {r^2} $ $ $
Thus, the area of regular octagon inscribed in a circle of given radius r $ = 2\sqrt 2 {r^2} $
So, the correct answer is “ $ = 2\sqrt 2 {r^2} $ ”.

Note: Given question is a typical problem involving a lot of geometrical concepts and analytical visualization. The question can be solved by various methods involving geometrical ideas and trigonometric formulae like sine and cosine rules.