Answer
398.4k+ views
Hint: We first form the area of $\Delta ABC$ as $ar\left( \Delta ABC \right)=ar\left( \Delta ACD \right)-ar\left( \Delta BCD \right)$. We take the right-angle triangles and find their areas. We subtract them to find the area of $\Delta ABC$.
Complete step-by-step solution:
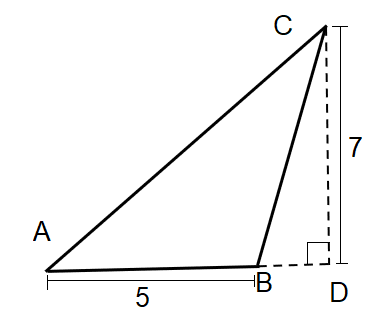
The given $\Delta ABC$, has a height of 7 cm.
We take the perpendicular point from point C on extended AB as D.
We assume the area of $\Delta ABC$ as $ar\left( \Delta ABC \right)=ar\left( \Delta ACD \right)-ar\left( \Delta BCD \right)$
As the $\angle ADC={{90}^{\circ }}$, therefore we can take both $\Delta ACD$ and $\Delta BCD$ as right-angled triangles.
The height for both of them will be $CD=7$.
Now let us assume the length $BD=a$. Therefore, $AD=AB+BD=5+a$.
Now we find the areas. The formula is half of the multiplication of the sides holding the right-angle.
For $\Delta ACD$, the area is $\dfrac{1}{2}\times AD\times CD=\dfrac{7\left( 5+a \right)}{2}$.
For $\Delta BCD$, the area is $\dfrac{1}{2}\times BD\times CD=\dfrac{7a}{2}$.
So, $ar\left( \Delta ABC \right)=ar\left( \Delta ACD \right)-ar\left( \Delta BCD \right)=\dfrac{7\left( 5+a \right)}{2}-\dfrac{7a}{2}$.
We simplify to get \[ar\left( \Delta ABC \right)=\dfrac{7}{2}\left( 5+a-a \right)=\dfrac{35}{2}=17.5c{{m}^{2}}\].
The correct option is (a).
Note: The height is necessarily needed to be inside the figure. The height on the extended line is also the height of the figure. In that case we can take the area for $\Delta ABC$ as $\dfrac{1}{2}\times AB\times CD=\dfrac{35}{2}$.
Complete step-by-step solution:
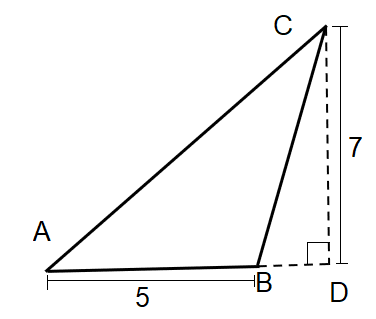
The given $\Delta ABC$, has a height of 7 cm.

We take the perpendicular point from point C on extended AB as D.
We assume the area of $\Delta ABC$ as $ar\left( \Delta ABC \right)=ar\left( \Delta ACD \right)-ar\left( \Delta BCD \right)$
As the $\angle ADC={{90}^{\circ }}$, therefore we can take both $\Delta ACD$ and $\Delta BCD$ as right-angled triangles.
The height for both of them will be $CD=7$.
Now let us assume the length $BD=a$. Therefore, $AD=AB+BD=5+a$.
Now we find the areas. The formula is half of the multiplication of the sides holding the right-angle.
For $\Delta ACD$, the area is $\dfrac{1}{2}\times AD\times CD=\dfrac{7\left( 5+a \right)}{2}$.
For $\Delta BCD$, the area is $\dfrac{1}{2}\times BD\times CD=\dfrac{7a}{2}$.
So, $ar\left( \Delta ABC \right)=ar\left( \Delta ACD \right)-ar\left( \Delta BCD \right)=\dfrac{7\left( 5+a \right)}{2}-\dfrac{7a}{2}$.
We simplify to get \[ar\left( \Delta ABC \right)=\dfrac{7}{2}\left( 5+a-a \right)=\dfrac{35}{2}=17.5c{{m}^{2}}\].
The correct option is (a).
Note: The height is necessarily needed to be inside the figure. The height on the extended line is also the height of the figure. In that case we can take the area for $\Delta ABC$ as $\dfrac{1}{2}\times AB\times CD=\dfrac{35}{2}$.
Recently Updated Pages
A key of a mechanical piano struck gently and then class 9 physics CBSE

Two spheres of masses m and M are situated in air and class 9 physics CBSE

A girl is carrying a school bag of 3 kg mass on her class 9 science CBSE

On the portion of the straight line x + 2y 4 intercepted class 11 maths JEE_Main

The equations of two equal sides AB AC of an isosceles class 11 maths JEE_Main

If two curves whose equations are ax2 + 2hxy + by2 class 11 maths JEE_Main

Trending doubts
Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

How do you graph the function fx 4x class 9 maths CBSE

Distinguish between the following Ferrous and nonferrous class 9 social science CBSE

What is pollution? How many types of pollution? Define it

Voters list is known as A Ticket B Nomination form class 9 social science CBSE

Which places in India experience sunrise first and class 9 social science CBSE