
Find the area of each shape correct to 1 decimal place (Use 3.14 for π).


Answer
510.3k+ views
Hint: In order to find the area of the given figure, we divide the figure into known figures for which the formula of area can be applied using the given dimensions. We divide the given figures into a rectangle and semi circles and apply their formulae of area respectively.
Complete step-by-step answer:
Given Data,
π = 3.14
We know, area of a rectangle is A = l × b, where l and b are the length and the breadth of the rectangle and the area of a semicircle is
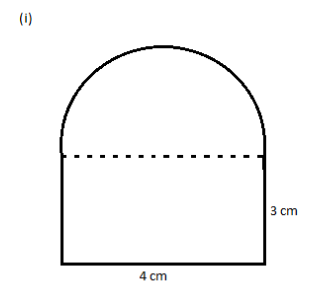
(i)
The given figure can be divided into a rectangle on the bottom part and a semi-circle on the top part. From the figure the dimensions of the rectangle are (3 × 4).
And from the figure, the diameter of the semicircle is equal to the length of the rectangle, 4 cm. Therefore the radius of the semicircle is half of it, i.e. r =
Now the area of this figure is given by
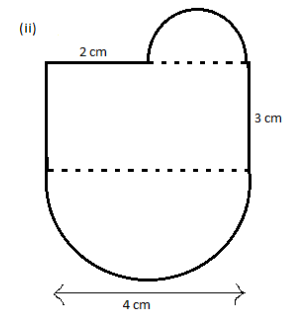
(ii)
The given figure can be divided into a semicircle on the bottom part and a semi-circle on the top part along with a rectangle in between them.
From the figure the dimensions of the rectangle are (3 × 4).
And from the figure, the diameter of the lower semicircle is equal to the length of the rectangle, 4 cm. Therefore the radius of the semicircle is half of it, i.e. r =
And from the figure, the diameter of the upper semicircle is equal to the length of the rectangle subtracted by 2 cm, i.e. 4 - 2 = 2 cm. Therefore the radius of the semicircle is half of it, i.e. r =
Now the area of this figure is given by
Therefore the area of figure (i) and (ii) are 18.28 sq cm and 19.85 sq cm respectively.
Note: In order to solve this type of question the key is to exactly know how to divide the given figure into geometrical shapes by looking at the figure. Then we determine the dimensions of the geometrical figures by comparing the new figure to the original figure.
In this question we directly wrote the formula of a semicircle by expressing it as half of the area of the circle. Figures given in this type of questions like these, we consider they are drawn to scale.
Area is always represented in square units.
Complete step-by-step answer:
Given Data,
π = 3.14
We know, area of a rectangle is A = l × b, where l and b are the length and the breadth of the rectangle and the area of a semicircle is
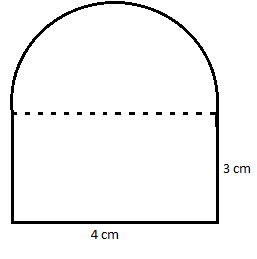
(i)

The given figure can be divided into a rectangle on the bottom part and a semi-circle on the top part. From the figure the dimensions of the rectangle are (3 × 4).
And from the figure, the diameter of the semicircle is equal to the length of the rectangle, 4 cm. Therefore the radius of the semicircle is half of it, i.e. r =
Now the area of this figure is given by
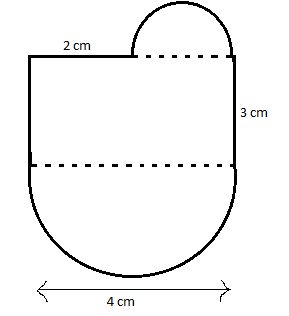
(ii)

The given figure can be divided into a semicircle on the bottom part and a semi-circle on the top part along with a rectangle in between them.
From the figure the dimensions of the rectangle are (3 × 4).
And from the figure, the diameter of the lower semicircle is equal to the length of the rectangle, 4 cm. Therefore the radius of the semicircle is half of it, i.e. r =
And from the figure, the diameter of the upper semicircle is equal to the length of the rectangle subtracted by 2 cm, i.e. 4 - 2 = 2 cm. Therefore the radius of the semicircle is half of it, i.e. r =
Now the area of this figure is given by
Therefore the area of figure (i) and (ii) are 18.28 sq cm and 19.85 sq cm respectively.
Note: In order to solve this type of question the key is to exactly know how to divide the given figure into geometrical shapes by looking at the figure. Then we determine the dimensions of the geometrical figures by comparing the new figure to the original figure.
In this question we directly wrote the formula of a semicircle by expressing it as half of the area of the circle. Figures given in this type of questions like these, we consider they are drawn to scale.
Area is always represented in square units.
Recently Updated Pages
Basicity of sulphurous acid and sulphuric acid are

Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Biology: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 4 Maths: Engaging Questions & Answers for Success

Trending doubts
Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Difference Between Plant Cell and Animal Cell

Given that HCF 306 657 9 find the LCM 306 657 class 9 maths CBSE

The highest mountain peak in India is A Kanchenjunga class 9 social science CBSE

What is the difference between Atleast and Atmost in class 9 maths CBSE

What is pollution? How many types of pollution? Define it




